dsphdl.ChannelSynthesizer
Description
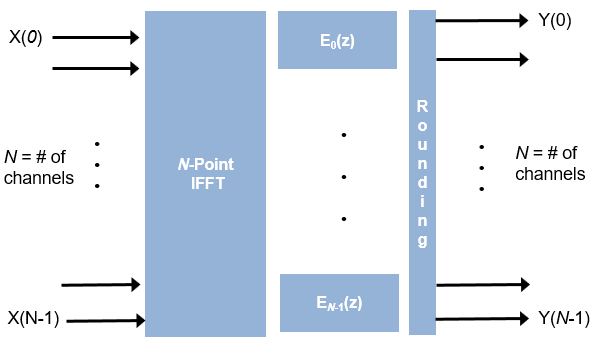
The dsphdl.ChannelSynthesizer
System object™ combines narrowband signals into a multi-channel signal using the polyphase
filter bank technique. The filter bank uses a prototype lowpass filter and is implemented
using a polyphase structure. You can specify the filter coefficients directly or through
design parameters. The System object provides an architecture suitable for HDL code generation and hardware
deployment.
The System object supports real and complex fixed-point inputs.
To combine multiple narrowband signals into a broadband signal:
Create the
dsphdl.ChannelSynthesizerobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Note
You can also generate HDL code for this hardware-optimized algorithm, without creating a MATLAB® script, by using the DSP HDL IP Designer app. The app provides the same interface and configuration options as the System object.
Creation
Syntax
Description
ChannelSynthesizer = dsphdl.ChannelSynthesizer
ChannelSynthesizer = dsphdl.ChannelSynthesizer(Name=Value)
Properties
Usage
Syntax
Description
[
combines the narrowband row input dataOut,validOut]
= channelsynthesizer(dataIn,validIn)dataIn vector signals and returns a
broadband signal, dataOut, when validIn is
1 (true). The validIn and
validOut arguments are logical scalars that indicate the validity
of the input and output signals, respectively.
[
combines the narrowband row input dataOut,validOut]
= channelsynthesizer(dataIn,validIn,reset)dataIn vector signals returns a
broadband signal, dataOut, when validIn is
1 (true) and reset is 0
(false). When reset is 1 (true), the object stops
the current calculation and clears all internal state.
To use this syntax, set the ResetInputPort property to true. For example:
synthesizer = dsphdl.ChannelSynthesizer(...,ResetInputPort=true); ... [dataOut,validOut] = synthesizer(dataIn,validIn,reset)
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
References
[1] Harris, Fredric J. Multirate Signal Processing for Communication Systems. Upper Saddle River, N.J: Prentice Hall PTR, 2004.
[2] Harris, Frederic J., Chris Dick, and Michael Rice. "Digital Receivers and Transmitters Using Polyphase Filter Banks for Wireless Communications." IEEE® Transactions on Microwave Theory and Techniques. 51, no 4, (April 2003): 1395–1412. https://doi.org/10.1109/TMTT.2003.809176.
Extended Capabilities
Version History
Introduced in R2021b