Channelizer

Polyphase filter bank and fast Fourier transform

• 

×

Libraries:
DSP HDL Toolbox / Filtering

Description

The Channelizer block separates a broadband input signal into multiple narrowband output signals. It provides hardware speed and area optimization for streaming data applications. The block accepts scalar or vector input of real or complex data, provides hardware-friendly control signals, and has optional output frame control signals. You can achieve gigasamples-per-second (GSPS) throughput, also called super sample rates, using vector input. The block implements a polyphase filter, with one subfilter per input vector element. The hardware implementation interleaves the subfilters, which results in sharing each filter multiplier (FFT Length / Input Size) times. The FFT implementation uses the same pipelined Radix 2^2 FFT algorithm as the FFT block.

Note

You can also generate HDL code for this hardware-optimized algorithm, without creating a Simulink^® model, by using the DSP HDL IP Designer app. The app provides the same interface and configuration options as the Simulink block.

Examples

High-Throughput Channelizer for FPGA

Implement a polyphase filter bank channelizer with throughput of gigasamples-per-second (GSPS).

• Open Script

HDL Implementation of Four Channel Synthesizer and Channelizer

Synthesize four stereo signals into a broadband signal and split the signal back into the individual narrowband signals.

• Open Script

Ports

Input

data — Input data

scalar or column vector of real or complex values

Input data, specified as a scalar or a column vector of real or complex values.

The vector size must be a power of 2 and in the range [2, 64], and is not greater than the number of channels (FFT length).

The software supports double and single data types for simulation, but not for HDL code generation.

The block does not accept uint64 data.

Data Types: fixed point | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | single | double
Complex Number Support: Yes

valid — Indicates valid input data

scalar

Control signal that indicates if the input data is valid. When valid is 1 (true), the block captures the values from the input data port. When valid is 0 (false), the block ignores the values from the input data port.

Data Types: Boolean

reset — Clears internal states

scalar

Control signal that clears internal states. When reset is 1 (true), the block stops the current calculation and clears internal states. When the reset is 0 (false) and the input valid is 1 (true), the block captures data for processing.

For more reset considerations, see the Reset Signal section on the Hardware Control Signals page.

Dependencies

To enable this port, on the Control Ports tab, select the Enable reset input port parameter.

Data Types: Boolean

Output

data — Frequency channel output data

vector

• If you set Output vector size to Same as number of frequency bands (default), the output data is a 1-by-M vector where M is the FFT length.

• If you set Output vector size to Same as input size, the output data is an M-by-1 vector where M is the input vector size.

The output order is bit natural for either output size. The output data type is a result of the Filter output and the bit growth in the FFT necessary to avoid overflow.

valid — Indicates valid output data

scalar

Control signal that indicates if the data from the output data port is valid. When valid is 1 (true), the block returns valid data from the output data port. When valid is 0 (false), the values from the output data port are not valid.

Data Types: Boolean

start — Indicates first valid cycle of output frame

scalar

Control signal that indicates the first valid cycle of the output frame.

When start is 1 (true), the block returns the first valid sample of the frame from the output data port.

Dependencies

To enable this port, on the Control Ports select the Enable start output port parameter.

Data Types: Boolean

end — Indicates last valid cycle of output frame

scalar

Control signal that indicates the last valid cycle of the output frame.

When end is 1 (true), the block returns the last valid sample of the frame from the output data port.

Dependencies

To enable this port, on the Control Ports select the Enable end output port parameter.

Data Types: Boolean

Parameters

Main

Filter coefficients — Polyphase filter coefficients

[ -0.032, 0.121, 0.318, 0.482, 0.546, 0.482, 0.318, 0.121, -0.032 ] (default) | vector of real or complex numeric values

If the number of coefficients is not a multiple of Number of frequency bands (FFT length), the block pads this vector with zeros. The default filter specification is a raised-cosine FIR filter, rcosdesign(0.25,2,4,'sqrt'). You can specify a vector of coefficients or a call to a filter design function that returns the coefficient values. By default, the block casts the coefficients to the same data type as the input.

Filter structure — HDL filter architecture

Direct form transposed (default) | Direct form systolic

Specify the HDL filter architecture as one of these structures:

• Direct form transposed — This architecture is a fully parallel implementation that is suitable for FPGA and ASIC applications. For architecture and performance details, see Fully Parallel Transposed Architecture.

• Direct form systolic — This architecture provides a fully parallel filter implementation that makes efficient use of Intel^® and Xilinx^® DSP blocks. For architecture and performance details, see Fully Parallel Systolic Architecture.

Number of frequency bands (FFT length) — FFT length

8 (default) | integer power of two

For HDL code generation, the FFT length must be a power of 2 from 2² to 2¹⁶.

Complex multiplication — HDL implementation of complex multipliers

Use 4 multipliers and 2 adders (default) | Use 3 multipliers and 5 adders

HDL implementation of complex multipliers, specified as either 'Use 4 multipliers and 2 adders' or 'Use 3 multipliers and 5 adders'. Depending on your synthesis tool and target device, one option may be faster or smaller.

Output vector size — Size of output data

Same as number of frequency bands (default) | Same as input size

The output data is a vector of M elements. The output order is bit natural for either output size.

• Same as number of frequency bands — Output data is a 1-by-M vector, where M is the FFT length.

• Same as input size — Output data is an M-by-1 vector, where M is the input vector size.

Divide butterfly outputs by two — FFT scaling

on (default) | off

When you select this parameter, the FFT implements an overall 1/N scale factor by scaling the result of each pipeline stage by 2. This adjustment keeps the output of the FFT in the same amplitude range as its input. If scaling is disabled, the FFT avoids overflow by increasing the word length by 1 bit at each stage.

Data Types

Rounding mode — Rounding method used for internal fixed-point calculations

Floor (default) | Ceiling | Convergent | Nearest | Round | Zero

See Rounding Modes. The block uses fixed-point arithmetic for internal calculations when the input is any integer or fixed-point data type. This option does not apply when the input is single or double. Each FFT stage rounds after the twiddle factor multiplication but before the butterflies. Rounding can also occur when casting the coefficients and the output of the polyphase filter to the data types you specify.

Saturate on integer overflow — Overflow handling for internal fixed-point calculations

off (default) | on

See Overflow Handling. The block uses fixed-point arithmetic for internal calculations when the input is any integer or fixed-point data type. This option does not apply when the input is single or double. This option applies to casting the coefficients and the output of the polyphase filter to the data types you specify.

The FFT algorithm avoids overflow by either scaling the output of each stage (Normalize enabled), or by increasing the word length by 1 bit at each stage (Normalize disabled).

Coefficients — Data type of the filter coefficients

Inherit: Same word length as input (default) | data type expression

The block casts the polyphase filter coefficients to this data type, using the rounding and overflow settings you specify. When you select Inherit: Same word length as input (default), the block selects the binary point using fi() best-precision rules.

Filter output — Data type of the output of the polyphase filter

Inherit: Same word length as input (default) | Inherit: via internal rule | data type expression

The block casts the output of the polyphase filter (the input to the FFT) to this data type, using the rounding and overflow settings you specify. When you select Inherit: via internal rule, the block selects a best-precision binary point by considering the values of your filter coefficients and the range of your input data type.

By default, the FFT logic does not modify the data type. When you disable Divide butterfly outputs by two, the FFT increases the word length by 1 bit at each stage to avoid overflow.

Control Ports

Enable reset input port — Optional reset signal

off (default) | on

When you select this parameter, the reset port shows on the block icon. When the reset input is true, the block stops calculation and clears all internal state.

Enable start output port — Optional control signal indicating start of data

off (default) | on

When you select this parameter, the start port shows on the block icon. The start signal is true for the first cycle of output data in a frame.

Enable end output port — Optional control signal indicating end of data

off (default) | on

When you select this parameter, the end port shows on the block icon. The end signal is true for the last cycle of output data in a frame.

Algorithms

The polyphase filter algorithm requires a subfilter for each FFT channel. For more detail on the polyphase filter architecture, refer to [1], and to the Channelizer (DSP System Toolbox) block reference page.

Note

The output of this block does not match the output from the Channelizer (DSP System Toolbox) block sample-for-sample. This mismatch is because the blocks apply the input samples to the subfilters in different orders. The Channelizer (DSP System Toolbox) block applies input X(0) to subfilter E_M-1(z), X(1) to subfilter E_M-2(z), ..., X(M-1) to subfilter E₀(z). The channels detected by both blocks match, when analyzed over multiple frames.

If the input vector size, M, is the same as the FFT length, N, then the block implements N subfilters in the hardware. Each subfilter is an FIR filter (Direct form transposed or Direct form systolic) with NumCoeffs/N taps.

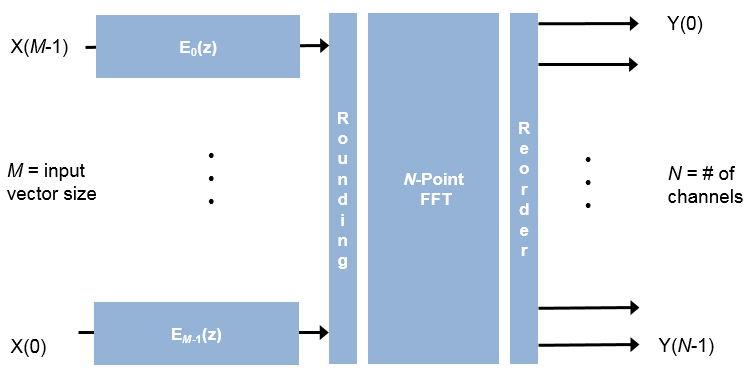
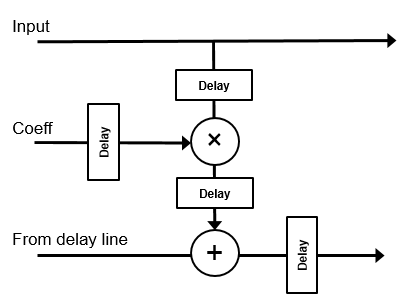
If the vector size is less than N, the block implements one subfilter for each input vector element. The subfilter multipliers are shared as necessary to implement N channel filters. The shared multiplier taps have a lookup table for N/M filter coefficients. Each tap is followed by a delay line of N/M–1 cycles.

The output of the subfilters is cast to the specified Filter output, using the rounding and overflow settings you chose. Each filter tap in the subfilter is pipelined to target the DSP sections of an FPGA.

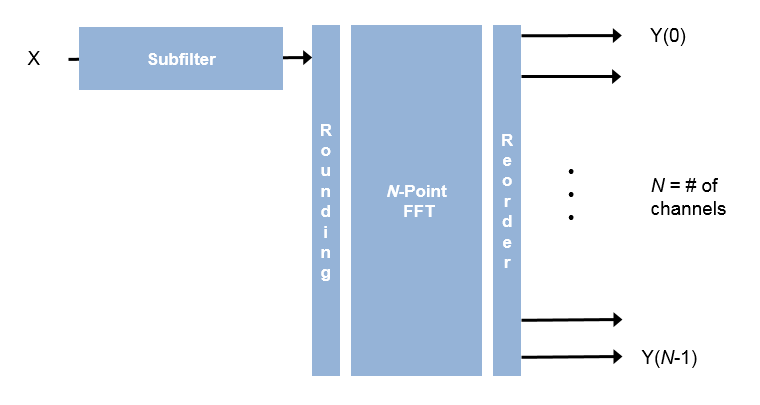
For instance, for an FFT length of 8, and an input vector size of 4, the block implements four filters. Each multiplier is shared N/M times, or twice. Each tap applies two coefficients, and the delay line is N/M–1 cycles.

For scalar input, the block implements one filter. Each multiplier is shared N times. Each tap applies N coefficients, and the delay line is N–1 cycles.

Latency

The latency varies with FFT length, vector size, and filter structure. After you update the model, the latency is displayed on the block icon. The displayed latency is the number of cycles between the first valid input and the first valid output, assuming that the input is contiguous. The filter coefficients do not affect the latency. Setting the output size equal to the input size reduces the latency, because the samples are not saved and reordered.

Control Signals

This diagram shows validIn and validOut signals for contiguous input data with a vector size of 16, an FFT length of 512, and when you select the Direct form transposed filter architecture. In this example, the output vector size is specified same as the input vector size.

The diagram also shows the optional startOut and endOut signals that indicate frame boundaries. When enabled, startOut pulses for one cycle with the first validOut of the frame, and endOut pulses for one cycle with the last validOut of the frame.

If you apply continuous input frames (no gap in validIn between frames), the output will also be continuous, after the initial latency.

The validIn signal can be noncontiguous. Data accompanied by a validIn signal is stored until a frame is filled. Then the data in output is a contiguous frame of N/M cycles. This diagram shows noncontiguous input and contiguous output for an FFT length of 512 and a vector size of 16 samples.

Performance

These resource and performance data are the place-and-route results from the generated HDL targeted to a Xilinx Zynq^®- 7000 ZC706 evaluation board. The three examples in the tables use this common configuration.

• FFT length (default) — 8

• Filter length — 96 coefficients

• Filter structure — Direct form transposed

• 16-bit complex input data

• Coefficient data type — Same word length as input

• Filter output data type — Same word length as input

• Complex multiplication — Use 4 multipliers and 2 adders

• Output scaling — Enabled

• Output vector size — Same as input size

Performance of the synthesized HDL code varies with your target and synthesis options.

For scalar input, the design achieves a clock frequency of 506.84 MHz. The latency is 51 cycles. The subfilters share each multiplier eight (N) times. The design uses these resources.

Resource	Number Used
LUT	2898
FFS	3746
Xilinx LogiCORE® DSP48	28

For four-sample vector input, the design achieves a clock frequency of 452 MHz. The latency is 37 cycles. The subfilters share each multiplier twice (N/M). The design uses these resources.

Resource	Number Used
LUT	1991
FFS	8305
Xilinx LogiCORE DSP48	104

For eight-sample vector input, the design achieves a clock frequency of 360 MHz. The latency is 18 cycles. When the input size is the same as the FFT length, the subfilters do not share any multipliers. The design uses these resources.

Resource	Number Used
LUT	1683
FFS	2992
Xilinx LogiCORE DSP48	208

References

[1] Harris, F. J., C. Dick, and M. Rice. “Digital Receivers and Transmitters Using Polyphase Filter Banks for Wireless Communications.” IEEE Transactions on Microwave Theory and Techniques. Vol. 51, No. 4, April 2003.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using Simulink® Coder™.

This block supports C/C++ code generation for Simulink accelerator and rapid accelerator modes and for DPI component generation.

HDL Code Generation

Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).

Version History

Introduced in R2017a

R2022a: Moved to DSP HDL Toolbox from DSP System Toolbox

Before R2022a, this block was named Channelizer HDL Optimized and was included in the DSP System Toolbox™ DSP System Toolbox HDL Support library.

R2022a: FFT length of 4

You can now set the FFT length to 4 (2²). In previous releases the FFT length had to be a power of 2 from 8 (2³) to 2¹⁶.

R2022a: Direct form systolic filter structure support

The block now supports fully parallel systolic architecture. To use this architecture, set the Filter structure parameter to Direct form systolic.