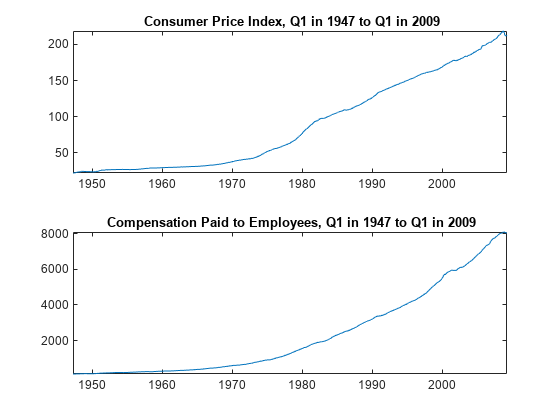
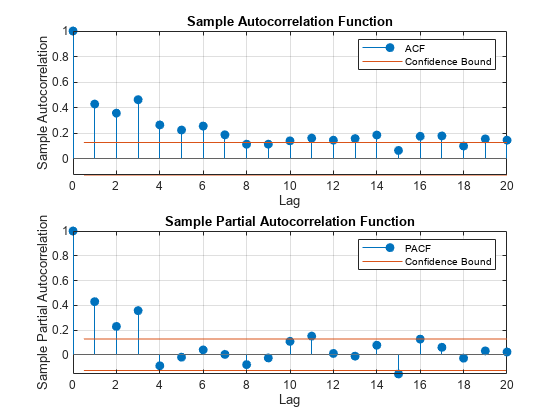
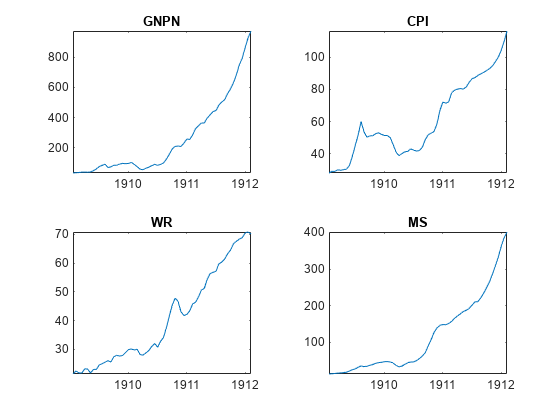
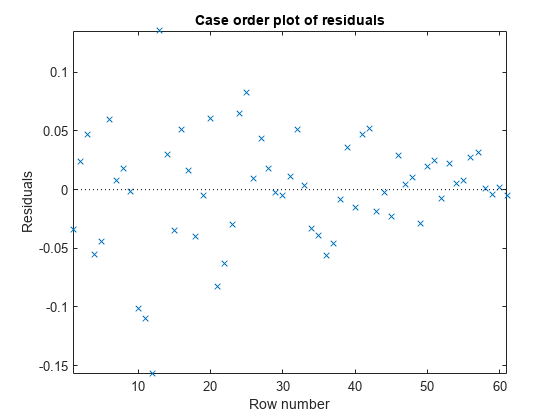
fgls
Feasible generalized least squares
Syntax
Description
[
returns vectors of coefficient estimates and corresponding standard errors, and the
estimated coefficient covariance matrix, from applying feasible generalized least squares (FGLS) to the multiple linear regression
model coeff,se,EstCoeffCov] = fgls(X,y)y = Xβ +
ε. y is a vector of response data and
X is a matrix of predictor data.
[
returns a table containing FGLS coefficient estimates and corresponding standard errors,
and a table containing the FGLS estimated coefficient covariance matrix, from applying
FGLS to the variables in the input table or timetable. The response variable in the
regression is the last variable, and all other variables are the predictor
variables.CoeffTbl,CovTbl] = fgls(Tbl)
To select a different response variable for the regression, use the
ResponseVariable name-value argument. To select different predictor
variables, use the PredictorNames name-value argument.
[___] = fgls(___,
specifies options using one or more name-value arguments in
addition to any of the input argument combinations in previous syntaxes.
Name=Value)fgls returns the output argument combination for the
corresponding input arguments.
For example,
fgls(Tbl,ResponseVariable="GDP",InnovMdl="H4",Plot="all") provides
coefficient, standard error, and residual mean-squared error (MSE) plots of iterations of
FGLS for a regression model with White’s robust innovations covariance, and the table
variable GDP is the response while all other variables are
predictors.
[___] = fgls(
plots on the axes specified in ax,___,Plot=plot)ax instead of the axes of new figures
when plot is not "off". ax can
precede any of the input argument combinations in the previous syntaxes.
[___,
returns handles to plotted graphics objects when iterPlots] = fgls(___,Plot=plot)plot is not
"off". Use elements of iterPlots to modify
properties of the plots after you create them.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Tips
To obtain standard generalized least squares (GLS) estimates:
To obtain weighted least squares (WLS) estimates, set the
InnovCov0name-value argument to a vector of inverse weights (e.g., innovations variance estimates).In specific models and with repeated iterations, scale differences in the residuals might produce a badly conditioned estimated innovations covariance and induce numerical instability. Conditioning improves when you set
ResCond=true.
Algorithms
In the presence of nonspherical innovations, GLS produces efficient estimates relative to OLS and consistent coefficient covariances, conditional on the innovations covariance. The degree to which
fglsmaintains these properties depends on the accuracy of both the model and estimation of the innovations covariance.Rather than estimate FGLS estimates the usual way,
fglsuses methods that are faster and more stable, and are applicable to rank-deficient cases.Traditional FGLS methods, such as the Cochrane-Orcutt procedure, use low-order, autoregressive models. These methods, however, estimate parameters in the innovations covariance matrix using OLS, where
fglsuses maximum likelihood estimation (MLE) [2].
References
[1] Cribari-Neto, F. "Asymptotic Inference Under Heteroskedasticity of Unknown Form." Computational Statistics & Data Analysis. Vol. 45, 2004, pp. 215–233.
[2] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[3] Judge, G. G., W. E. Griffiths, R. C. Hill, H. Lϋtkepohl, and T. C. Lee. The Theory and Practice of Econometrics. New York, NY: John Wiley & Sons, Inc., 1985.
[4] Kutner, M. H., C. J. Nachtsheim, J. Neter, and W. Li. Applied Linear Statistical Models. 5th ed. New York: McGraw-Hill/Irwin, 2005.
[5] MacKinnon, J. G., and H. White. "Some Heteroskedasticity-Consistent Covariance Matrix Estimators with Improved Finite Sample Properties." Journal of Econometrics. Vol. 29, 1985, pp. 305–325.
[6] White, H. "A Heteroskedasticity-Consistent Covariance Matrix and a Direct Test for Heteroskedasticity." Econometrica. Vol. 48, 1980, pp. 817–838.
Version History
Introduced in R2014bSee Also
Functions
Objects
Topics
- Classical Model Misspecification Tests
- Time Series Regression I: Linear Models
- Time Series Regression VI: Residual Diagnostics
- Time Series Regression X: Generalized Least Squares and HAC Estimators
- Autocorrelation and Partial Autocorrelation
- Engle’s ARCH Test
- Nonspherical Models
- Time Series Regression Models