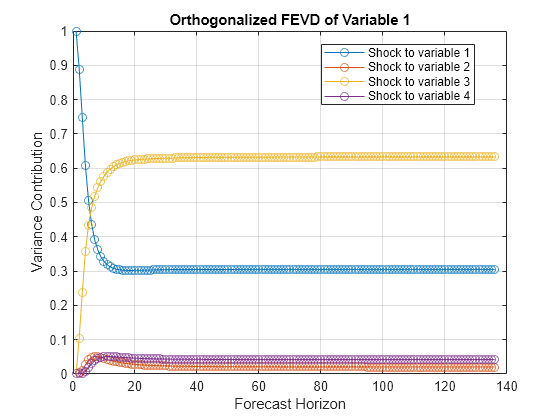
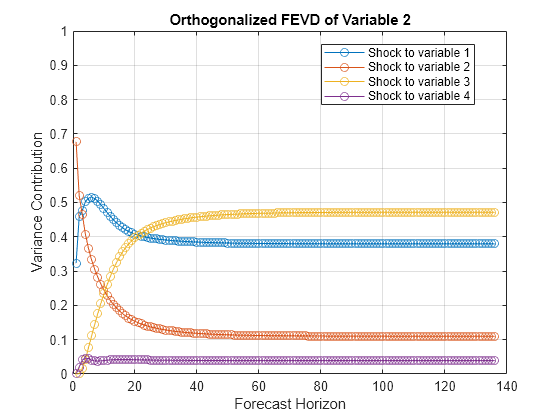
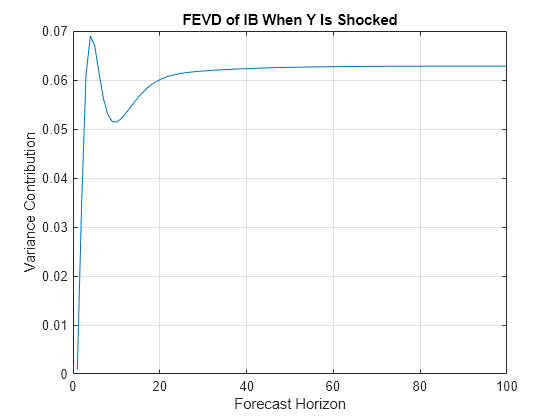
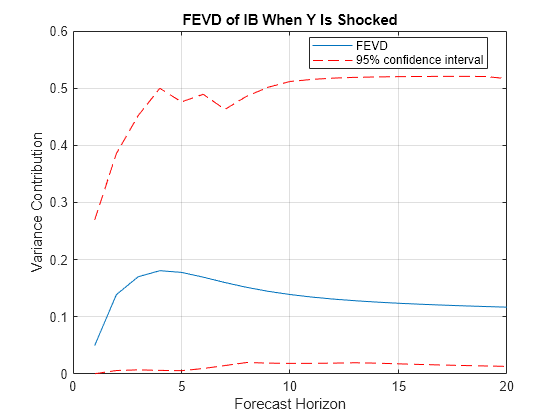
fevd
Generate vector autoregression (VAR) model forecast error variance decomposition (FEVD)
Syntax
Description
The fevd function returns the forecast error variance decomposition (FEVD) of the variables in a VAR(p) model attributable to shocks to each response variable in the system. A fully specified varm model object characterizes the VAR model.
To estimate or plot the FEVD of a dynamic linear model characterized by structural, autoregression, or moving average coefficient matrices, see armafevd.
The FEVD provides information about the relative importance of each innovation in affecting the forecast error variance of all response variables in the system. In contrast, the impulse response function (IRF) traces the effects of an innovation shock to one variable on the response of all variables in the system. To estimate the IRF of a VAR model characterized by a varm model object, see irf.
You can supply optional data, such as a presample, as a numeric array, table, or
timetable. However, all specified input data must be the same data type. When the input model
is estimated (returned by estimate), supply the same data type as the data
used to estimate the model. The data type of the outputs matches the data type of the
specified input data.
Decomposition = fevd(Mdl)Mdl, characterized by a
fully specified varm model object.
fevd shocks variables at time 0, and returns the FEVD for
times 1 through 20.
If Mdl is an estimated model (returned by estimate) fit to a numeric matrix of input response data, this syntax
applies.
Decomposition = fevd(Mdl,Name=Value)fevd returns numeric arrays when all optional input data are
numeric arrays. For example, fevd(Mdl,NumObs=10,Method="generalized")
specifies estimating a generalized FEVD for periods 1 through 10.
If Mdl is an estimated model fit to a numeric matrix of input
response data, this syntax applies.
[
returns numeric arrays of lower Decomposition,Lower,Upper] = fevd(___)Lower and upper
Upper 95% confidence bounds for confidence intervals on the true
FEVD, for each period and variable in the FEVD, using any input argument combination in
the previous syntaxes. By default, fevd estimates confidence
bounds by conducting Monte Carlo simulation.
If Mdl is an estimated model fit to a numeric matrix of input
response data, this syntax applies.
If Mdl is a custom varm model object (an object not returned by estimate or modified after estimation), fevd can
require a sample size for the simulation SampleSize or presample
responses Y0.
Tbl = fevd(___)Tbl containing the FEVDs and, optionally, corresponding
95% confidence bounds, of the response variables that compose the
VAR(p) model Mdl. The variables in
Tbl correspond to the variables in the system shocked at time 0.
Each variable contains a matrix with columns corresponding to the FEVDs of the variables
in the system. (since R2022b)
If you set at least one name-value argument that controls the 95% confidence bounds on
the FEVD, Tbl also contains a variable for each of the lower and
upper bounds. For example, Tbl contains confidence bounds when you
set the NumPaths name-value argument.
If Mdl is an estimated model fit to a table or timetable of input
response data, this syntax applies.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Algorithms
If
Methodis"orthogonalized", thenfevdorthogonalizes the innovation shocks by applying the Cholesky factorization of the model covariance matrixMdl.Covariance. The covariance of the orthogonalized innovation shocks is the identity matrix, and the FEVD of each variable sums to one (that is, the sum along any row ofDecompositionor rows associated with FEVD variables inTblis one). Therefore, the orthogonalized FEVD represents the proportion of forecast error variance attributable to various shocks in the system. However, the orthogonalized FEVD generally depends on the order of the variables.If
Methodis"generalized", then the resulting FEVD is invariant to the order of the variables, and is not based on an orthogonal transformation. Also, the resulting FEVD sums to one for a particular variable only whenMdl.Covarianceis diagonal [4]. Therefore, the generalized FEVD represents the contribution to the forecast error variance of equation-wise shocks to the response variables in the model.If
Mdl.Covarianceis a diagonal matrix, then the resulting generalized and orthogonalized FEVDs are identical. Otherwise, the resulting generalized and orthogonalized FEVDs are identical only when the first variable inMdl.SeriesNamesshocks all variables (for example, all else being the same, both methods yield the same value ofDecomposition(:,1,:)).The predictor data in
XorInSamplerepresents a single path of exogenous multivariate time series. If you specifyXorInSampleand the modelMdlhas a regression component (Mdl.Betais not an empty array),fevdapplies the same exogenous data to all paths used for confidence interval estimation.fevdconducts a simulation to estimate the confidence boundsLowerandUpperor associated variables inTbl.If you do not specify residuals by supplying
Eor usingInSample,fevdconducts a Monte Carlo simulation by following this procedure:Simulate
NumPathsresponse paths of lengthSampleSizefromMdl.Fit
NumPathsmodels that have the same structure asMdlto the simulated response paths. IfMdlcontains a regression component and you specify predictor data by supplyingXor usingInSample,fevdfits theNumPathsmodels to the simulated response paths and the same predictor data (the same predictor data applies to all paths).Estimate
NumPathsFEVDs from theNumPathsestimated models.For each time point t = 0,…,
NumObs, estimate the confidence intervals by computing 1 –ConfidenceandConfidencequantiles (the upper and lower bounds, respectively).
Otherwise,
fevdconducts a nonparametric bootstrap by following this procedure:Resample, with replacement,
SampleSizeresiduals fromEorInSample. Perform this stepNumPathstimes to obtainNumPathspaths.Center each path of bootstrapped residuals.
Filter each path of centered, bootstrapped residuals through
Mdlto obtainNumPathsbootstrapped response paths of lengthSampleSize.Complete steps 2 through 4 of the Monte Carlo simulation, but replace the simulated response paths with the bootstrapped response paths.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Lütkepohl, H. "Asymptotic Distributions of Impulse Response Functions and Forecast Error Variance Decompositions of Vector Autoregressive Models." Review of Economics and Statistics. Vol. 72, 1990, pp. 116–125.
[3] Lütkepohl, Helmut. New Introduction to Multiple Time Series Analysis. New York, NY: Springer-Verlag, 2007.
[4] Pesaran, H. H., and Y. Shin. "Generalized Impulse Response Analysis in Linear Multivariate Models." Economic Letters. Vol. 58, 1998, pp. 17–29.