irf
Generate vector autoregression (VAR) model impulse responses
Syntax
Description
The irf function returns the dynamic response, or the impulse response
function (IRF), to a one-standard-deviation shock to each variable in a VAR(p)
model. A fully specified varm model object characterizes the VAR
model.
To estimate or plot the IRF of a dynamic linear model characterized by structural,
autoregression, or moving average coefficient matrices, see armairf.
IRFs trace the effects of an innovation shock to one variable on the response of all
variables in the system. In contrast, the forecast error variance decomposition (FEVD)
provides information about the relative importance of each innovation in affecting all
variables in the system. To estimate the FEVD of a VAR model characterized by a
varm model object, see fevd.
You can supply optional data, such as a presample, as a numeric array, table, or
timetable. However, all specified input data must be the same data type. When the input model
is estimated (returned by estimate), supply the same data type as the data
used to estimate the model. The data type of the outputs matches the data type of the
specified input data.
Response = irf(Mdl)Mdl, characterized by a
fully specified varm model object.
irf shocks variables at time 0, and returns the IRF for
times 0 through 19.
If Mdl is an estimated model (returned by estimate) fit to a numeric matrix of input response data, this syntax
applies.
Response = irf(Mdl,Name=Value)irf(Mdl,NumObs=10,Method="generalized") specifies estimating a
generalized IRF for 10 time points starting at time 0, during which
irf applies the shock.
If Mdl is an estimated model fit to a numeric matrix of input
response data, this syntax applies.
[
returns numeric arrays of lower Response,Lower,Upper] = irf(___)Lower and upper
Upper 95% confidence bounds for confidence intervals on the true
IRF, for each period and variable in the IRF, using any input argument combination in the
previous syntaxes. By default, irf estimates confidence
bounds by conducting Monte Carlo simulation.
If Mdl is an estimated model fit to a numeric matrix of input
response data, this syntax applies.
If Mdl is a custom varm model object (an object not returned by estimate or modified after estimation), irf can
require a sample size for the simulation SampleSize or presample
responses Y0.
Tbl = irf(___)Tbl containing the IRFs and, optionally, corresponding 95%
confidence bounds, of the response variables that compose the VAR(p)
model Mdl. The variables in Tbl correspond to the
variables in the system shocked at time 0. Each variable contains a matrix with columns
corresponding to the IRFs of the variables in the system. (since R2022b)
If you set at least one name-value argument that controls the 95% confidence bounds on
the IRF, Tbl also contains a variable for each of the lower and upper
bounds. For example, Tbl contains confidence bounds when you set the
NumPaths name-value argument.
If Mdl is an estimated model fit to a table or timetable of input
response data, this syntax applies.
Examples
Fit a 4-D VAR(2) model to Danish money and income rate series data in a numeric matrix. Then, estimate and plot the orthogonalized IRF from the estimated model.
Load the Danish money and income data set.
load Data_JDanishFor more details on the data set, enter Description at the command line.
Assuming that the series are stationary, create a varm model object that represents a 4-D VAR(2) model. Specify the variable names.
Mdl = varm(4,2); Mdl.SeriesNames = DataTable.Properties.VariableNames;
Mdl is a varm model object specifying the structure of a 4-D VAR(2) model; it is a template for estimation.
Fit the VAR(2) model to the numeric matrix of time series data Data.
Mdl = estimate(Mdl,Data);
Mdl is a fully specified varm model object representing an estimated 4-D VAR(2) model.
Estimate the orthogonalized IRF from the estimated VAR(2) model.
Response = irf(Mdl);
Response is a 20-by-4-by-4 array representing the IRF of Mdl. Rows correspond to consecutive time points from time 0 to 19, columns correspond to variables receiving a one-standard-deviation innovation shock at time 0, and pages correspond to responses of variables to the variable being shocked. Mdl.SeriesNames specifies the variable order.
Display the IRF of the bond rate (variable 3, IB) when the log of real income (variable 2, Y) is shocked at time 0.
Response(:,2,3)
ans = 20×1
0.0018
0.0048
0.0054
0.0051
0.0040
0.0029
0.0019
0.0011
0.0006
0.0003
0.0001
-0.0000
-0.0001
-0.0001
-0.0001
⋮
Plot the IRFs of all series on separate plots by passing the estimated AR coefficient matrices and innovations covariance matrix of Mdl to armairf.
armairf(Mdl.AR,[],InnovCov=Mdl.Covariance);
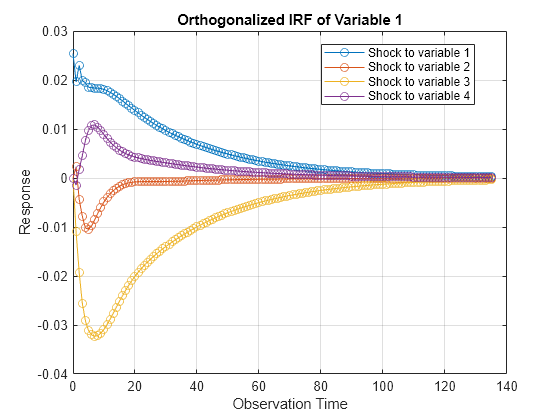
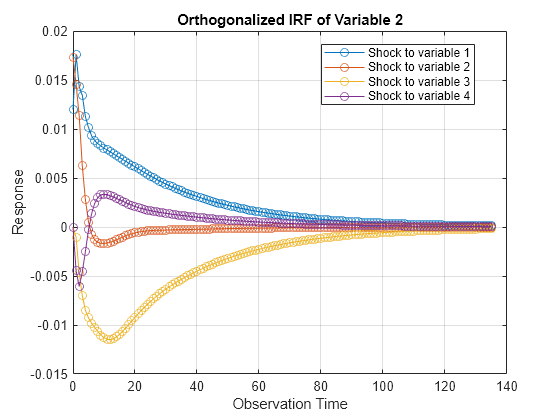

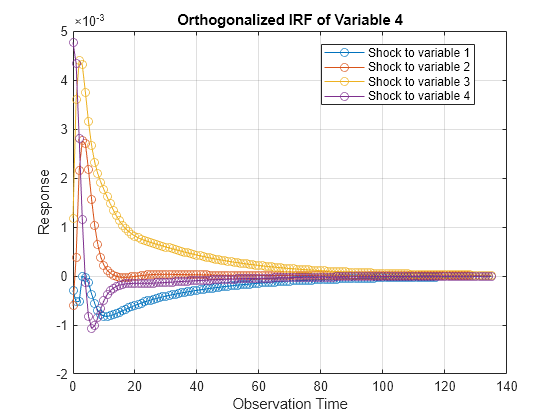
Each plot shows the four IRFs of a variable when all other variables are shocked at time 0. Mdl.SeriesNames specifies the variable order.
Consider the 4-D VAR(2) model in Specify Data in Numeric Matrix When Plotting IRF. Estimate the generalized IRF of the system for 50 periods.
Load the Danish money and income data set, and then estimate the VAR(2) model.
load Data_JDanish
Mdl = varm(4,2);
Mdl.SeriesNames = DataTable.Properties.VariableNames;
Mdl = estimate(Mdl,DataTable.Series);Estimate the generalized IRF from the estimated VAR(2) model.
Response = irf(Mdl,Method="generalized",NumObs=50);Response is a 50-by-4-by-4 array representing the generalized IRF of Mdl.
Plot the generalized IRF of the bond rate when real income is shocked at time 0.
figure; plot(0:49,Response(:,2,3)) title("IRF of IB When Y Is Shocked") xlabel("Observation Time") ylabel("Response") grid on
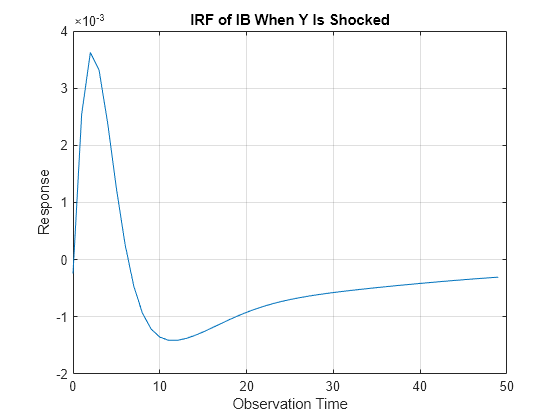
The bond rate fades slowly when real income is shocked at time 0.
Since R2022b
Fit a 4-D VAR(2) model to Danish money and income rate series data in a numeric matrix. Then, estimate and plot the orthogonalized IRF from the estimated model.
Load the Danish money and income data set.
load Data_JDanishThe data set includes four time series in the timetable DataTimeTable. For more details on the data set, enter Description at the command line.
Assuming that the series are stationary, create a varm model object that represents a 4-D VAR(2) model. Specify the variable names.
Mdl = varm(4,2); Mdl.SeriesNames = DataTimeTable.Properties.VariableNames;
Mdl is a varm model object specifying the structure of a 4-D VAR(2) model; it is a template for estimation.
Fit the VAR(2) model to the data set.
EstMdl = estimate(Mdl,DataTimeTable);
Mdl is a fully specified varm model object representing an estimated 4-D VAR(2) model.
Estimate the orthogonalized IRF and corresponding 95% confidence intervals from the estimated VAR(2) model. To return confidence intervals, you must set a name-value argument that controls confidence intervals, for example, Confidence. Set Confidence to 0.95.
rng(1); % For reproducibility
Tbl = irf(EstMdl,Confidence=0.95);
size(Tbl)ans = 1×2
20 12
Tbl
Tbl=20×12 timetable
Time M2_IRF Y_IRF IB_IRF ID_IRF M2_IRF_LowerBound Y_IRF_LowerBound IB_IRF_LowerBound ID_IRF_LowerBound M2_IRF_UpperBound Y_IRF_UpperBound IB_IRF_UpperBound ID_IRF_UpperBound
___________ _____________________________________________________ _______________________________________________________ ___________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ ______________________________________________________ _______________________________________________________ _____________________________________________________ ___________________________________________________ ____________________________________________________ ___________________________________________________
01-Jul-1974 0.025385 0.011979 -0.0030299 -0.00029592 0 0.017334 0.0017985 -0.00060941 0 0 0.0072384 0.0011766 0 0 0 0.0047648 0.017729 0.0062931 -0.0046236 -0.0012223 0 0.012192 -0.00017736 -0.0016259 0 0 0.0046542 -0.00050518 0 0 0 0.00322 0.02713 0.016442 -0.00074788 0.0010392 0 0.019303 0.0037597 0.00088073 0 0 0.0080468 0.002298 0 0 0 0.0049936
01-Oct-1974 0.019597 0.017604 -0.0024059 -0.00052605 0.0022668 0.014588 0.0047558 0.00037877 -0.011013 -0.0010791 0.0096387 0.0036033 -0.0014511 -0.0044686 -1.6666e-05 0.0043446 0.0088617 0.0075327 -0.0054155 -0.0024484 -0.0045762 0.0055602 0.00085487 -0.0014949 -0.015821 -0.0059937 0.0044639 0.00097209 -0.0072913 -0.0092174 -0.0021639 0.001595 0.024652 0.020779 0.00056005 0.0014407 0.0069932 0.017056 0.0070093 0.0021859 -0.0048396 0.0046483 0.010957 0.0051531 0.0043279 0.00045888 0.0017342 0.0050611
01-Jan-1975 0.023011 0.01432 -0.0014045 -0.00051972 -0.0043703 0.011341 0.005376 0.0021556 -0.019326 -0.0046725 0.010182 0.004395 0.0017534 -0.0060605 -0.0011601 0.002806 0.011414 0.0045521 -0.004882 -0.0024604 -0.01291 -0.00094466 -0.00017957 -0.00068506 -0.021662 -0.011 0.0035604 0.0011887 -0.0069887 -0.01257 -0.0045524 -0.00041328 0.029914 0.016987 0.0018906 0.0011012 0.0051311 0.013943 0.0080383 0.0041762 -0.0068581 0.003094 0.012053 0.0057324 0.0082731 0.0013124 0.0025533 0.0042406
01-Apr-1975 0.019864 0.01344 -0.0014933 -4.4254e-06 -0.0078183 0.0062247 0.0050662 0.0027626 -0.025548 -0.0070059 0.009493 0.0043074 0.0045597 -0.004589 -0.002223 0.0011591 0.0063539 0.0025976 -0.0054684 -0.0021938 -0.017355 -0.0064979 -0.00123 0.00010743 -0.029292 -0.013974 0.0015562 0.00077995 -0.0081444 -0.011287 -0.0062556 -0.0022002 0.028924 0.015926 0.0014925 0.0012851 0.0059606 0.011209 0.0080886 0.0047651 -0.0063978 0.0028959 0.012097 0.0057966 0.014418 0.0038715 0.0033635 0.0023838
01-Jul-1975 0.019419 0.011244 -0.0015969 -3.4305e-05 -0.010187 0.0028147 0.0039998 0.0026985 -0.029124 -0.0084906 0.0084798 0.0037481 0.0077423 -0.0025063 -0.0026634 -0.00013404 0.005327 -0.00049621 -0.0054593 -0.0021455 -0.022716 -0.0081187 -0.0028733 -0.00042378 -0.034992 -0.015799 0.00056474 0.00020164 -0.0078458 -0.010846 -0.0068023 -0.0035519 0.029407 0.014405 0.001692 0.0015767 0.0087664 0.010134 0.0075162 0.0043343 -0.0057691 0.0018746 0.012047 0.0055231 0.020043 0.0064893 0.0029097 0.001343
01-Oct-1975 0.018532 0.01016 -0.0019436 -0.00013964 -0.010448 0.00049217 0.0028587 0.0021692 -0.031107 -0.0092773 0.0074784 0.0031474 0.0097242 -0.00029442 -0.0026358 -0.00082626 0.001818 -0.0004023 -0.0058779 -0.0022755 -0.023734 -0.0077482 -0.0042795 -0.00098779 -0.038594 -0.016547 -0.00011469 -0.00064435 -0.0095859 -0.0070065 -0.0059945 -0.0034737 0.030136 0.013705 0.0016763 0.0017479 0.011566 0.0082498 0.0057995 0.0033017 -0.0044473 0.0013279 0.011642 0.0050999 0.022978 0.0090112 0.0027824 0.0014644
01-Jan-1976 0.018426 0.0092868 -0.0022099 -0.00036763 -0.0097658 -0.00071481 0.0018519 0.0015618 -0.032019 -0.0098054 0.0066319 0.002661 0.010735 0.0013489 -0.0022958 -0.001066 0.00094487 -0.0010919 -0.0057706 -0.0026426 -0.023367 -0.0091729 -0.0049467 -0.0014946 -0.042002 -0.016681 -0.00084973 -0.0010919 -0.010268 -0.0059067 -0.0046107 -0.0030697 0.030831 0.014467 0.0020979 0.0014645 0.013995 0.0070356 0.0042604 0.0028084 -0.0042527 0.0021613 0.010919 0.0047273 0.024747 0.010363 0.0021819 0.00073538
01-Apr-1976 0.018347 0.0088274 -0.002408 -0.00055954 -0.0085284 -0.0013241 0.0011035 0.001029 -0.032301 -0.010245 0.0059331 0.0023208 0.010834 0.0024299 -0.0018575 -0.0010181 0.00088792 -0.00087384 -0.0057043 -0.0027239 -0.022321 -0.0095626 -0.0046415 -0.0016955 -0.044772 -0.015403 -0.0014757 -0.00074988 -0.010505 -0.0057904 -0.0042961 -0.0025666 0.030874 0.015059 0.0021942 0.0012385 0.01511 0.0075202 0.0041588 0.0022807 -0.0018926 0.0020667 0.0099711 0.0041106 0.027227 0.010447 0.0026554 0.0011517
01-Jul-1976 0.018349 0.0085007 -0.0025003 -0.00070381 -0.0072023 -0.0015783 0.00059083 0.00064004 -0.032139 -0.010662 0.0053454 0.0020863 0.010389 0.0030152 -0.0014396 -0.00084984 0.00081535 -0.00056917 -0.0054989 -0.0027904 -0.020095 -0.0090132 -0.003905 -0.0019258 -0.046259 -0.016859 -0.0018945 -0.0010315 -0.0088981 -0.0047543 -0.0042238 -0.0017878 0.030856 0.014085 0.0023174 0.0013691 0.017564 0.0079639 0.0040872 0.0017655 -0.001588 0.0020803 0.0088559 0.0036667 0.02646 0.010048 0.0026267 0.0012534
01-Oct-1976 0.018261 0.0082681 -0.0025175 -0.00078515 -0.0059528 -0.0016715 0.000265 0.00038128 -0.031642 -0.01103 0.0048331 0.0019104 0.0096565 0.0032746 -0.0011032 -0.00066034 -0.0011251 -0.00075733 -0.0050727 -0.0026529 -0.019957 -0.0091831 -0.0037003 -0.0015265 -0.046571 -0.018406 -0.0023099 -0.0010146 -0.0087836 -0.0043276 -0.0035229 -0.0015206 0.031925 0.013921 0.0023499 0.0013534 0.017285 0.0080779 0.0037871 0.0016071 0.00034958 0.0018116 0.0082019 0.0031525 0.025188 0.0098717 0.0023763 0.001372
01-Jan-1977 0.018088 0.0080578 -0.0024803 -0.00082067 -0.004866 -0.0016783 6.7351e-05 0.00021975 -0.030874 -0.011308 0.0043776 0.0017587 0.0088385 0.0033353 -0.00085828 -0.00049952 -0.0023654 -0.00054861 -0.0046959 -0.0023017 -0.018881 -0.0083688 -0.0036323 -0.0013151 -0.045822 -0.019143 -0.0022457 -0.00076165 -0.0096651 -0.0046474 -0.0033535 -0.001605 0.031832 0.013992 0.0023109 0.0011487 0.01618 0.0079136 0.0033058 0.0015065 0.0014169 0.0019553 0.0074233 0.0026903 0.023693 0.0092439 0.0022507 0.0010427
01-Apr-1977 0.01782 0.0078585 -0.0024126 -0.00082488 -0.0039472 -0.0016348 -4.6051e-05 0.00012029 -0.029898 -0.011467 0.0039728 0.0016154 0.0080434 0.0032901 -0.00069265 -0.00038034 -0.0041445 -0.0009108 -0.0046233 -0.0021475 -0.017842 -0.0074943 -0.0036166 -0.0012714 -0.044148 -0.019166 -0.0023327 -0.00078836 -0.010263 -0.0046773 -0.0028019 -0.001797 0.030983 0.013903 0.0022172 0.001152 0.014886 0.007478 0.0027978 0.0013601 0.0017628 0.0019984 0.0059992 0.0024748 0.023083 0.0093155 0.0021594 0.00090656
01-Jul-1977 0.01748 0.0076612 -0.0023288 -0.00081178 -0.0031853 -0.0015527 -0.00010551 5.8177e-05 -0.028778 -0.011497 0.0036184 0.001477 0.007324 0.0031905 -0.00058632 -0.00029882 -0.0055294 -0.00154 -0.0045625 -0.0019225 -0.017729 -0.00744 -0.0034336 -0.0012351 -0.041703 -0.018635 -0.0029266 -0.00097794 -0.010567 -0.004571 -0.0030526 -0.00144 0.029897 0.013651 0.002083 0.0011265 0.015725 0.0067952 0.0028631 0.0012628 0.0032766 0.0021382 0.0054534 0.00231 0.021 0.0091161 0.00197 0.000865
01-Oct-1977 0.017084 0.0074669 -0.0022386 -0.00078982 -0.0025611 -0.0014412 -0.00012965 1.837e-05 -0.027577 -0.01141 0.003315 0.0013467 0.0066953 0.0030638 -0.00052096 -0.00024515 -0.0059883 -0.0019006 -0.0045009 -0.0017518 -0.016735 -0.0070905 -0.0030476 -0.0012138 -0.03866 -0.017655 -0.0023904 -0.0010579 -0.010714 -0.0044868 -0.0030057 -0.0010935 0.028693 0.01332 0.0015194 0.0010569 0.016655 0.0061735 0.0029008 0.0010539 0.0049304 0.0023071 0.0052074 0.0022951 0.019005 0.008691 0.0018979 0.00088102
01-Jan-1978 0.016649 0.007275 -0.0021468 -0.00076393 -0.0020585 -0.0013098 -0.00013023 -6.9227e-06 -0.02635 -0.011223 0.0030608 0.0012284 0.006156 0.0029232 -0.00048251 -0.00021015 -0.0067654 -0.0016931 -0.0044291 -0.0016366 -0.016779 -0.0072429 -0.0028373 -0.0011991 -0.035195 -0.016242 -0.0025182 -0.0010499 -0.010659 -0.0043064 -0.002775 -0.0010409 0.028206 0.01294 0.0015156 0.00095142 0.016305 0.0058332 0.0026818 0.00094436 0.0054449 0.0022641 0.0053236 0.0021337 0.018369 0.0079906 0.0017187 0.00082592
01-Apr-1978 0.016187 0.0070851 -0.0020565 -0.00073641 -0.0016627 -0.0011692 -0.00011514 -2.1687e-05 -0.025141 -0.010963 0.0028515 0.001125 0.0056974 0.0027764 -0.00046133 -0.00018714 -0.0053812 -0.0015885 -0.0043428 -0.0016435 -0.016571 -0.007324 -0.0025033 -0.0011496 -0.033556 -0.015142 -0.0025535 -0.0010552 -0.010407 -0.0040787 -0.0025947 -0.0011176 0.027675 0.012605 0.0015485 0.00082164 0.015764 0.0056146 0.0024931 0.0010281 0.0054922 0.0019958 0.0054463 0.0021499 0.019244 0.0078422 0.00157 0.00071951
⋮
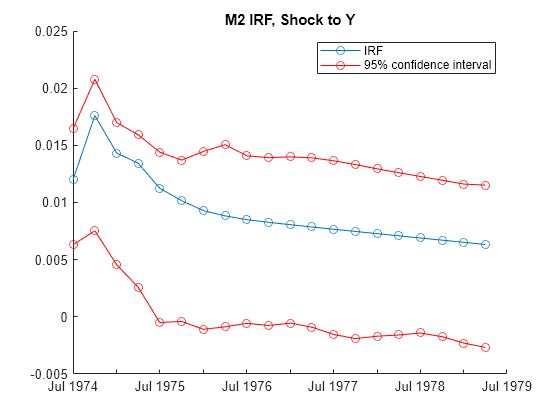
Tbl is a timetable with 20 rows, representing the periods in the IRF, and 12 variables. Each variable is a 20-by-4 matrix of the IRF or confidence bound associated with a variable in the model EstMdl. For example, Tbl.M2_IRF(:,2) is the IRF of Mdl.SeriesNames(2), which is the variable Y, resulting from a one-standard-deviation shock on 01-Jul-1974 (period 0) to M2. [Tbl.M2_IRF_LowerBound(:,2),Tbl.M2_IRF_UpperBound(:,2)] are the corresponding 95% confidence intervals.
Plot the IRF of Y and its 95% confidence interval resulting from a one-standard-deviation shock on 01-Jul-1974 to M2.
idxM2 = startsWith(Tbl.Properties.VariableNames,"M2"); M2IRF = Tbl(:,idxM2); shockIdx = 2; figure hold on plot(M2IRF.Time,M2IRF.M2_IRF(:,shockIdx),"-o") plot(M2IRF.Time,[M2IRF.M2_IRF_LowerBound(:,shockIdx) ... M2IRF.M2_IRF_UpperBound(:,shockIdx)],"-o",Color="r") legend("IRF","95% confidence interval") title("Y IRF, Shock to M2") hold off
Consider the 4-D VAR(2) model in Specify Data in Numeric Matrix When Plotting IRF. Estimate and plot its orthogonalized IRF and 95% Monte Carlo confidence intervals on the true IRF.
Load the Danish money and income data set, then estimate the VAR(2) model.
load Data_JDanish
Mdl = varm(4,2);
Mdl.SeriesNames = DataTable.Properties.VariableNames;
Mdl = estimate(Mdl,DataTable.Series);Estimate the IRF and corresponding 95% Monte Carlo confidence intervals from the estimated VAR(2) model.
rng(1); % For reproducibility
[Response,Lower,Upper] = irf(Mdl);Response, Lower, and Upper are 20-by-4-by-4 arrays representing the orthogonalized IRF of Mdl and corresponding lower and upper bounds of the confidence intervals. For all arrays, rows correspond to consecutive time points from time 0 to 19, columns correspond to variables receiving a one-standard-deviation innovation shock at time 0, and pages correspond to responses of variables to the variable being shocked. Mdl.SeriesNames specifies the variable order.
Plot the orthogonalized IRF with its confidence bounds of the bond rate when real income is shocked at time 0.
irfshock2resp3 = Response(:,2,3); IRFCIShock2Resp3 = [Lower(:,2,3) Upper(:,2,3)]; figure; h1 = plot(0:19,irfshock2resp3); hold on h2 = plot(0:19,IRFCIShock2Resp3,"r--"); legend([h1 h2(1)],["IRF" "95% Confidence Interval"]) xlabel("Time Index"); ylabel("Response"); title("IRF of IB When Y Is Shocked"); grid on hold off
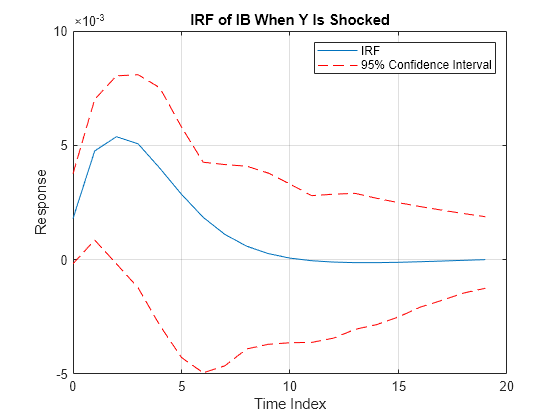
The effect of the impulse to real income on the bond rate fades after 10 periods.
Consider the 4-D VAR(2) model in Specify Data in Numeric Matrix When Plotting IRF. Estimate and plot its orthogonalized IRF and 90% bootstrap confidence intervals on the true IRF.
Load the Danish money and income data set, and then estimate the VAR(2) model. Return the residuals from model estimation.
load Data_JDanish Mdl = varm(4,2); Mdl.SeriesNames = DataTable.Properties.VariableNames; [Mdl,~,~,Res] = estimate(Mdl,DataTable.Series); T = size(DataTable,1) % Total sample size
T = 55
n = size(Res,1) % Effective sample sizen = 53
Res is a 53-by-4 array of residuals. Columns correspond to the variables in Mdl.SeriesNames. The estimate function requires Mdl.P = 2 observations to initialize a VAR(2) model for estimation. Because presample data (Y0) is unspecified, estimate takes the first two observations in the specified response data to initialize the model. Therefore, the resulting effective sample size is T – Mdl.P = 53, and rows of Res correspond to the observation indices 3 through T.
Estimate the orthogonalized IRF and corresponding 90% bootstrap confidence intervals from the estimated VAR(2) model. Draw 500 paths of length n from the series of residuals.
rng(1); % For reproducibility
[Response,Lower,Upper] = irf(Mdl,E=Res,NumPaths=500,Confidence=0.9);Plot the orthogonalized IRF with its confidence bounds of the bond rate when real income is shocked at time 0.
irfshock2resp3 = Response(:,2,3); IRFCIShock2Resp3 = [Lower(:,2,3) Upper(:,2,3)]; figure; h1 = plot(0:19,irfshock2resp3); hold on h2 = plot(0:19,IRFCIShock2Resp3,"r--"); legend([h1 h2(1)],["IRF" "90% confidence interval"]) xlabel("Time Index") ylabel("Response") title("IRF of IB When Y Is Shocked"); grid on hold off
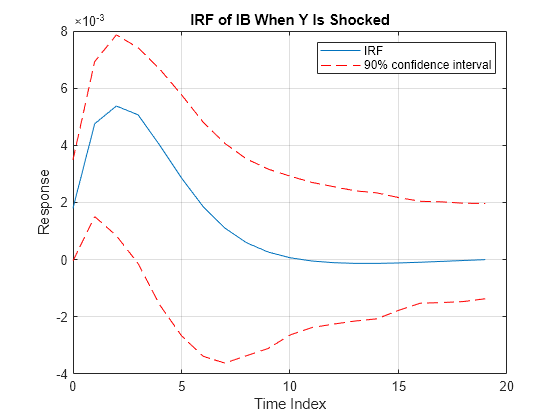
The effect of the impulse to real income on the bond rate fades after 10 periods.
Input Arguments
VAR model, specified as a varm model object created by varm or estimate. Mdl must be fully specified.
If Mdl is an estimated model (returned by estimate) , you must supply any optional data using the same data type as the input response data, to which the model is fit.
If Mdl is a custom varm model object (an object not returned by estimate or modified after estimation), irf can require a sample size for the simulation SampleSize or presample responses Y0.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: irf(Mdl,NumObs=10,Method="generalized") specifies estimating
a generalized IRF for 10 time points starting at time 0, during which
irf applies the shock.
Options for All IRFs
Number of periods for which irf computes
the IRF, specified as a positive integer.
NumObs specifies the number of
observations to include in the IRF (the number of rows in
Response or
Tbl).
Example: NumObs=10 specifies the inclusion of 10
time points in the IRF starting at time 0, during which
irf applies the shock,
and ending at period 9.
Data Types: double
IRF computation method, specified as a value in this table.
| Value | Description |
|---|---|
"orthogonalized" | Compute impulse responses using orthogonalized,
one-standard-deviation innovation shocks.
irf uses the Cholesky factorization of
Mdl.Covariance for orthogonalization. |
"generalized" | Compute impulse responses using one-standard-deviation innovation shocks. |
Example: Method="generalized"
Data Types: string | char
Options for Confidence Bound Estimation
Number of sample paths (trials) to generate, specified as a positive integer.
Example: NumPaths=1000 generates 1000 sample
paths from which the software derives the confidence bounds.
Data Types: double
Number of observations for the Monte Carlo simulation or bootstrap per sample path, specified as a positive integer.
Example: If you specify SampleSize=100 and do not specify the
E name-value argument, the software estimates confidence bounds
from NumPaths random paths of length 100 from
Mdl.
Example: If you specify SampleSize=100,E=Res, the software
resamples, with replacement, 100 observations (rows) from
Res to form a sample path of innovations to filter through
Mdl. The software forms NumPaths random
sample paths from which it derives confidence bounds.
Data Types: double
Presample response data that provides initial values for model estimation during the
simulation, specified as a numpreobs-by-numseries
numeric matrix. Use Y0 only in the following situations:
numpreobs is the number of presample observations.
numseries is Mdl.NumSeries, the dimensionality of the
input model.
Each row is a presample observation, and measurements in each row occur simultaneously.
The last row contains the latest presample observation. numpreobs is the
number of specified presample responses and it must be at least Mdl.P. If
you supply more rows than necessary, irf uses the latest
Mdl.P observations only.
numseries is the dimensionality of the input VAR model
Mdl.NumSeries. Columns must correspond to the response variables in
Mdl.SeriesNames.
The following situations determine the default or whether presample response data is required.
Data Types: double
Since R2022b
Presample data that provides initial values for the model Mdl,
specified as a table or timetable with numprevars variables and
numpreobs rows. Use Presample only in the
following situations:
Each row is a presample observation, and measurements in each row occur
simultaneously. numpreobs must be at least Mdl.P.
If you supply more rows than necessary, irf uses the latest
Mdl.P observations only.
Each variable is a numpreobs numeric vector representing one path.
To control presample variable selection, see the optional
PresampleResponseVariables name-value argument.
If Presample is a timetable, all the following conditions must be true:
Presamplemust represent a sample with a regular datetime time step (seeisregular).The datetime vector of sample timestamps
Presample.Timemust be ascending or descending.
If Presample is a table, the last row contains the latest
presample observation.
The following situations determine the default or whether presample response data is required.
If
Mdlis an unmodified estimated model,irfsetsPresampleto the presample response data used for estimation by default (see thePresamplename-value argument ofestimate).If
Mdlis a custom model (for example, you modify a model after estimation by using dot notation) and you return confidence bounds in the table or timetableTbl, you must specifyPresample.
Since R2022b
Variables to select from Presample to use for presample data, specified
as one of the following data types:
String vector or cell vector of character vectors containing
numseriesvariable names inPresample.Properties.VariableNamesA length
numseriesvector of unique indices (integers) of variables to select fromPresample.Properties.VariableNamesA length
numprevarslogical vector, wherePresampleResponseVariables(selects variablej) = truejPresample.Properties.VariableNames, andsum(PresampleResponseVariables)isnumseries
PresampleResponseVariables applies only when you specify
Presample.
The selected variables must be numeric vectors and cannot contain missing values
(NaN).
PresampleResponseNames does not need to contain the same names as in
Mdl.SeriesNames; irf uses the data in
selected variable PresampleResponseVariables(
as a presample for j)Mdl.SeriesNames(.j)
If the number of variables in Presample matches
Mdl.NumSeries, the default specifies all variables in
Presample. If the number of variables in Presample
exceeds Mdl.NumSeries, the default matches variables in
Presample to names in Mdl.SeriesNames.
Example: PresampleResponseVariables=["GDP" "CPI"]
Example: PresampleResponseVariables=[true false true false] or
PresampleResponseVariable=[1 3] selects the first and third table
variables for presample data.
Data Types: double | logical | char | cell | string
Predictor data xt for
estimating the model regression component during the simulation, specified as a numeric matrix
containing numpreds columns. Use X only in the following situations:
numpreds is the number of predictor variables
(size(Mdl.Beta,2)).
Each row corresponds to an observation, and measurements in each row
occur simultaneously. The last row contains the latest
observation. X must have at least
SampleSize rows. If you supply
more rows than necessary, irf uses
only the latest observations. irf
does not use the regression component in the presample
period.
Columns correspond to individual predictor variables. All predictor variables are present in the regression component of each response equation.
To maintain model consistency when irf
estimates the confidence bounds, specify predictor data when Mdl has a
regression component. If Mdl is an estimated model, specify the predictor
data used during model estimation (see the X name-value argument of estimate).
By default, irf excludes the regression
component from confidence bound estimation, regardless of its
presence in Mdl.
Data Types: double
Series of residuals from which to draw bootstrap samples, specified as a
numperiods-by-numseries numeric matrix.
irf assumes that E is free of serial
correlation. Use E only in the following situations:
Each column is the residual series corresponding to the response series names in
Mdl.SeriesNames.
Each row corresponds to a period in the FEVD and the corresponding confidence bounds.
If Mdl is an estimated varm model object (an object returned by estimate), you can specify E as the inferred
residuals from estimation (see the E output argument of
estimate or infer).
By default, irf derives confidence bounds by conducting a
Monte Carlo simulation.
Data Types: double
Since R2022b
Time series data containing numvars variables, including
numseries variables of residuals
et to bootstrap or
numpreds predictor variables
xt for the model regression component,
specified as a table or timetable. Use InSample only in the
following situations:
Each variable is a single path of observations, which irf
applies to all NumPaths sample paths. If you specify
Presample, you must specify which variables are residuals and
predictors. See the ResidualVariables and
PredictorVariables name-value arguments.
Each row is an observation, and measurements in each row occur simultaneously.
InSample must have at least SampleSize
rows. If you supply more rows than necessary, irf uses only
the latest observations.
If InSample is a timetable, the following conditions apply:
InSamplemust represent a sample with a regular datetime time step (seeisregular).The datetime vector
InSample.Timemust be ascending or descending.Presamplemust immediately precedeInSample, with respect to the sampling frequency.
If InSample is a table, the last row contains the latest
observation.
By default, irf derives confidence bounds by conducting a
Monte Carlo simulation and does not use the regression component, regardless of its
presence in Mdl.
Since R2022b
Variables to select from InSample to treat as residuals for
bootstrapping, specified as one of the following data types:
String vector or cell vector of character vectors containing
numseriesvariable names inInSample.Properties.VariableNamesA length
numseriesvector of unique indices (integers) of variables to select fromInSample.Properties.VariableNamesA length
numvarslogical vector, whereResidualVariables(selects variablej) = truejInSample.Properties.VariableNames, andsum(ResidualVariables)isnumseries
Regardless, selected residual variable
jMdl.SeriesNames(.j)
The selected variables must be numeric vectors and cannot contain missing values
(NaN).
By default, irf derives confidence bounds by conducting a
Monte Carlo simulation.
Example: ResidualVariables=["GDP_Residuals"
"CPI_Residuals"]
Example: ResidualVariables=[true false true false] or
ResidualVariable=[1 3] selects the first and third table variables as the
disturbance variables.
Data Types: double | logical | char | cell | string
Since R2022b
Variables to select from InSample to treat as exogenous predictor
variables xt, specified as one of the following data types:
String vector or cell vector of character vectors containing
numpredsvariable names inInSample.Properties.VariableNamesA length
numpredsvector of unique indices (integers) of variables to select fromInSample.Properties.VariableNamesA length
numvarslogical vector, wherePredictorVariables(selects variablej) = truejInSample.Properties.VariableNames, andsum(PredictorVariables)isnumpreds
Regardless, selected predictor variable
jMdl.Beta(:,.j)
PredictorVariables applies only when you specify
InSample.
The selected variables must be numeric vectors and cannot contain missing values
(NaN).
By default, irf excludes the regression component, regardless
of its presence in Mdl.
Example: PredictorVariables=["M1SL" "TB3MS" "UNRATE"]
Example: PredictorVariables=[true false true false] or
PredictorVariable=[1 3] selects the first and third table variables as
the response variables.
Data Types: double | logical | char | cell | string
Confidence level for the confidence bounds, specified as a numeric scalar in the interval [0,1].
For each period, randomly drawn confidence intervals cover the true response 100*Confidence% of the time.
The default value is 0.95, which implies that the confidence bounds represent 95% confidence intervals.
Example: Confidence=0.9 specifies 90% confidence
intervals.
Data Types: double
Note
NaNvalues inY0,X, andEindicate missing data.irfremoves missing data from these arguments by list-wise deletion. For each argument, if a row contains at least oneNaN,irfremoves the entire row.List-wise deletion reduces the sample size, can create irregular time series, and can cause
EandXto be unsynchronized.irfissues an error when any table or timetable input contains missing values.
Output Arguments
IRF of each variable, returned as a
numobs-by-numseries-by-numseries
numeric array. numobs is the value of NumObs.
Columns and pages correspond to the response variables in
Mdl.SeriesNames.
irf returns Response only in the
following situations:
You supply optional data inputs as numeric matrices.
Mdlis an estimated model fit to a numeric matrix of response data.
Response( is the
impulse response of variable t +
1,j,k)ktjtnumObs – 1, jnumseries, and
knumseries. For example,
Response(1,2,3) is the impulse response of variable
Mdl.SeriesName(3) at time
tMdl.SeriesName(2).
Lower confidence bounds, returned as a
numobs-by-numseries-by-numseries
numeric array. Elements of Lower correspond to elements of
Response.
irf returns Lower only in the
following situations:
You supply optional data inputs as numeric matrices.
Mdlis an estimated model fit to a numeric matrix of response data.
Lower( is the
lower bound of the t +
1,j,k)100*Confidence-th percentile interval on the
true impulse response of variable ktjLower(1,2,3) is the lower bound of the confidence interval on the
true impulse response of variable Mdl.SeriesName(3) at time
tMdl.SeriesName(2).
Upper confidence bounds, returned as a
numobs-by-numseries-by-numseries
numeric array. Elements of Upper correspond to elements of
Response.
irf returns Upper only in the
following situations:
You supply optional data inputs as numeric matrices.
Mdlis an estimated model fit to a numeric matrix of response data.
Upper( is the
upper bound of the t +
1,j,k)100*Confidence-th percentile interval on the
true impulse response of variable ktjUpper(1,2,3) is the upper bound of the confidence interval on the
true impulse response of variable Mdl.SeriesName(3) at time
tMdl.SeriesName(2).
Since R2022b
IRF and confidence bounds, returned as a table or timetable with
numobs rows. irf returns
Tbl only in the following situations:
You supply optional data inputs as tables or timetables.
Mdlis an estimated model fit to response data in a table or timetable.
Regardless, the data type of Tbl is the same as the
data type of specified data.
Variables in Tbl represent those response series being
shocked at time 0.
Variables containing IRFs have the following qualities:
For each response series in
Mdl.SeriesNames,irfnames the corresponding variableResponseJ_IRFResponseJMdl.Series(isj)GDP, the variableGDP_IRFcontains the IRFs of all response series resulting from a shock toGDPat time 0.Each variable contains a
numobs-by-numseriesnumeric matrix of resulting IRFs of all response series.numobsis the value ofNumObsandnumseriesis the value ofMdl.NumSeries.ResponseJ_IRF(is the impulse response of variablet+ 1,k)ktResponseJtnumObs– 1,Jnumseries, andknumseries.
When you set at least one name-value argument that controls the confidence bounds,
irfreturns the lower and upper confidence bounds on the true IRF of the response series. Variables containing the IRF confidence bounds have the following qualities:For each IRF
ResponseJ_IRFirfnames the corresponding lower and upper bound variablesResponseJ_IRF_LowerBoundResponseJ_IRF_UpperBoundResponseJGDP,GDP_IRF,Tblcontains variables for the corresponding lower and upper confidence boundsGDP_IRF_LowerBoundandGDP_IRF_UpperBound.Each confidence bound variable contains a
numobs-by-numseriesnumeric matrix.(
ResponseJ_IRF_LowerBound(t,k)ResponseJ_IRF_UpperBound(t,k)100*Confidence-th percentile confidence interval on the IRF of response seriesktResponseJtnumobs– 1,Jnumseries, andknumseries.
If Tbl is a timetable, the row order of Tbl,
either ascending or descending, matches the row order of InSample,
when you specify it. If you do not specify InSample and you specify
Presample, the row order of Tbl is the
same as the row order of Presample.
More About
An impulse response function (IRF) of a time series model (or dynamic response of the system) measures the changes in the future responses of all variables in the system when a variable is shocked by an impulse. In other words, the IRF at time t is the derivative of the responses at time t with respect to an innovation at time t0 (the time that innovation was shocked), t ≥ t0.
Consider a numseries-D VAR(p)
model for the multivariate response variable
yt. In lag operator notation, the infinite lag
MA representation of yt is
The general form of the IRF of yt shocked by an impulse to variable j by one standard deviation of its innovation m periods into the future is
ej is a selection vector of length
numseriescontaining a 1 in element j and zeros elsewhere.For the orthogonalized IRF, where P is the lower triangular factor in the Cholesky factorization of Σ, and Ωm is the lag m coefficient of Ω(L).
For the generalized IRF, where σj is the standard deviation of innovation j.
The IRF is free of the model constant, regression component, and time trend.
A vector autoregression (VAR) model is a stationary multivariate time series model consisting of a system of m equations of m distinct response variables as linear functions of lagged responses and other terms.
A VAR(p) model in difference-equation notation and in reduced form is
yt is a
numseries-by-1 vector of values corresponding tonumseriesresponse variables at time t, where t = 1,...,T. The structural coefficient is the identity matrix.c is a
numseries-by-1 vector of constants.Φj is a
numseries-by-numseriesmatrix of autoregressive coefficients, where j = 1,...,p and Φp is not a matrix containing only zeros.xt is a
numpreds-by-1 vector of values corresponding tonumpredsexogenous predictor variables.β is a
numseries-by-numpredsmatrix of regression coefficients.δ is a
numseries-by-1 vector of linear time-trend values.εt is a
numseries-by-1 vector of random Gaussian innovations, each with a mean of 0 and collectively anumseries-by-numseriescovariance matrix Σ. For t ≠ s, εt and εs are independent.
Condensed and in lag operator notation, the system is
where , Φ(L)yt is
the multivariate autoregressive polynomial, and I is the
numseries-by-numseries identity matrix.
Algorithms
If
Methodis"orthogonalized", then the resulting IRF depends on the order of the variables in the time series model. IfMethodis"generalized", then the resulting IRF is invariant to the order of the variables. Therefore, the two methods generally produce different results.If
Mdl.Covarianceis a diagonal matrix, then the resulting generalized and orthogonalized IRFs are identical. Otherwise, the resulting generalized and orthogonalized IRFs are identical only when the first variable shocks all variables (for example, all else being the same, both methods yield the same value ofResponse(:,1,:)).The predictor data in
XorInSamplerepresents a single path of exogenous multivariate time series. If you specifyXorInSampleand the modelMdlhas a regression component (Mdl.Betais not an empty array),irfapplies the same exogenous data to all paths used for confidence interval estimation.irfconducts a simulation to estimate the confidence boundsLowerandUpperor associated variables inTbl.If you do not specify residuals by supplying
Eor usingInSample,irfconducts a Monte Carlo simulation by following this procedure:Simulate
NumPathsresponse paths of lengthSampleSizefromMdl.Fit
NumPathsmodels that have the same structure asMdlto the simulated response paths. IfMdlcontains a regression component and you specify predictor data by supplyingXor usingInSample, thenirffits theNumPathsmodels to the simulated response paths and the same predictor data (the same predictor data applies to all paths).Estimate
NumPathsIRFs from theNumPathsestimated models.For each time point t = 0,…,
NumObs, estimate the confidence intervals by computing 1 –ConfidenceandConfidencequantiles (upper and lower bounds, respectively).
Otherwise,
irfconducts a nonparametric bootstrap by following this procedure:Resample, with replacement,
SampleSizeresiduals fromEorInSample. Perform this stepNumPathstimes to obtainNumPathspaths.Center each path of bootstrapped residuals.
Filter each path of centered, bootstrapped residuals through
Mdlto obtainNumPathsbootstrapped response paths of lengthSampleSize.Complete steps 2 through 4 of the Monte Carlo simulation, but replace the simulated response paths with the bootstrapped response paths.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Lütkepohl, Helmut. New Introduction to Multiple Time Series Analysis. New York, NY: Springer-Verlag, 2007.
[3] Pesaran, H. H., and Y. Shin. "Generalized Impulse Response Analysis in Linear Multivariate Models." Economic Letters. Vol. 58, 1998, pp. 17–29.
Version History
Introduced in R2019aIn addition to accepting input data in numeric arrays,
irf accepts input data in tables and timetables. irf chooses default series on which to operate, but you can use the following name-value arguments to select variables.
Presamplespecifies the input table or regular timetable of presample response data.PresampleResponseVariablesspecifies the response series names fromPresample.Insamplespecifies the table or regular timetable of residual and predictor data to compute bootstrap estimates.ResidualVariablesspecifies the residual series names inInSample.PredictorVariablesspecifies the predictor series inInSamplefor a model regression component.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)