Gate Valve (TL)
Gate valve in a thermal liquid system
Libraries:
Simscape /
Fluids /
Thermal Liquid /
Valves & Orifices /
Flow Control Valves
Description
The Gate Valve (TL) block represents a gate valve in a thermal liquid network. The valve comprises a round, sharp-edged orifice and a round gate with the same diameter. The gate opens or closes according to the displacement signal at port S. A positive signal lifts the gate to open the valve. The diagram shows the relationship between the opening area and the net displacement of the gate.
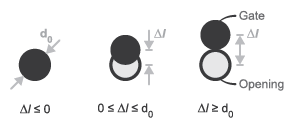
A smoothing function allows the valve opening area to change smoothly between the fully closed and fully open positions. The smoothing function reduces the abrupt opening area changes at the zero and maximum gate positions.
Mass Balance
The mass conservation equation in the valve is
where:
is the mass flow rate into the valve through port A.
is the mass flow rate into the valve through port B.
Momentum Balance
The momentum conservation equation in the valve is
where:
pA and pB are the pressures at port A and port B.
is the mass flow rate.
is the critical mass flow rate:
ρAvg is the average liquid density.
Cd is the discharge coefficient.
S is the valve inlet area.
PRLoss is the pressure ratio:
Energy Balance
The energy conservation equation in the valve is
where:
ϕA is the energy flow rate into the valve through port A.
ϕB is the energy flow rate into the valve through port B.
Valve Opening Area
The block computes the valve opening area by using the expression
where:
A is the valve opening area.
Aleak is the value of the Leakage area parameter.
d0 is the valve orifice diameter.
ACovered is the portion of the valve orifice area covered by the gate:
Δl is the net displacement of the gate center relative to the orifice center.
Smin is value of the Gate position when fully covering orifice parameter specified in the block dialog box.
Sd is the gate displacement specified through physical signal input port S.
Numerically Smoothed Displacement
When the valve is in a near-open or near-closed position,
you can maintain numerical robustness in your simulation by adjusting the
Smoothing factor parameter. If the Smoothing
factor parameter is nonzero, the block smoothly saturates the gate
displacement between 0 and the Valve orifice
diameter parameter. For more information, see Numerical Smoothing.
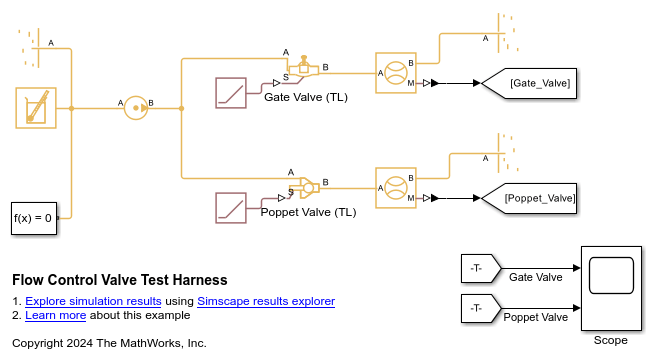
Examples
Ports
Input
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2016a