pdeval
Interpolate numerical solution of PDE
Description
[
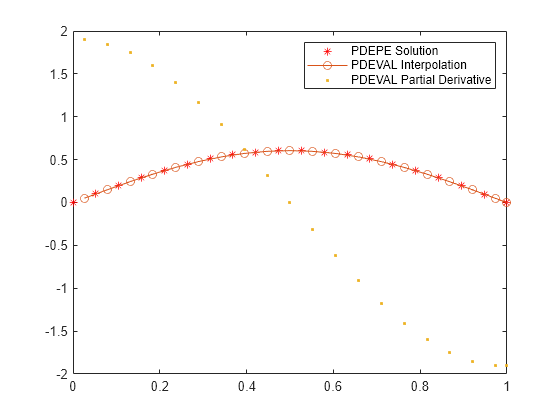
interpolates a numerical solution returned by u,dudx] = pdeval(m,xmesh,usol,xq)pdepe at new query points
xq, and returns the interpolated values of the solution
u and their partial derivative dudx. The
m, xmesh, and usol arguments are
reused from a previous call to pdepe:
The numerical solution produced by
sol = pdepe(m,@pdefun,@pdeic,@pdebc,xmesh,tspan)uses the coordinate symmetrymand spatial meshxmeshto return a 3-D matrix of the solution valuessol. Reuse themandxmeshinputs used to calculate the solution when you callpdeval.The input vector
usol = sol(i,:,k)is the value of componentkof the solution at timetspan(i). When there is only one solution component,usolis a row extracted from the solution matrixusol = sol(i,:).
Examples
Input Arguments
Output Arguments
Tips
pdevalevaluates the partial derivative rather than the flux . Although the flux is continuous, the partial derivative can have a jump at a material interface.
Extended Capabilities
Version History
Introduced before R2006a