Improving Control Performance with Look-Ahead (Previewing)
This example shows how to design a model predictive controller with look-ahead (previewing) on reference and measured disturbance trajectories.
Define Plant Model
Define the plant model as a linear time invariant system with two inputs (one manipulated variable and one measured disturbance) and one output.
plant = ss(tf({1,1},{[1 .5 1],[1 1]}),'min');
Get the state-space matrices of the plant model, set a sampling time of 0.2 s, get the discrete-time matrices, and specify the initial condition.
[A,B,C,D] = ssdata(plant); % continuous time ss realization Ts = 0.2; % sampling time [Ad,Bd,Cd,Dd] = ssdata(c2d(plant,Ts)); % discrete time ss realization x0 = [0;0;0]; % initial condition
Design Model Predictive Controller
Define type of input signals.
plant = setmpcsignals(plant,'MV',1,'MD',2);
Create the mpc object.
p = 20; % prediction horizon m = 10; % control horizon mpcobj = mpc(plant,Ts,p,m); % Specify MV constraints. mpcobj.MV = struct('Min',0,'Max',2); % Specify weights mpcobj.Weights = struct('MV',0,'MVRate',0.1,'Output',1);
-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000. -->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000. -->"Weights.OutputVariables" is empty. Assuming default 1.00000.
Simulate Closed Loop Using the sim Command
Tstop = 30; % simulation time. time = (0:Ts:(Tstop+p*Ts))'; % time vector r = double(time>10); % reference signal v = -double(time>20); % measured disturbance signal
Use the mpcsimopt object to turn on previewing feature in the closed-loop simulation.
params = mpcsimopt(mpcobj); params.MDLookAhead='on'; params.RefLookAhead='on';
Simulate in MATLAB® with the MPC Toolbox sim command.
YY1 = sim(mpcobj,Tstop/Ts+1,r,v,params);
-->Converting model to discrete time. -->Assuming output disturbance added to measured output #1 is integrated white noise. -->"Model.Noise" is empty. Assuming white noise on each measured output.
Simulate Using the mpcmove Command
Create array to store the closed-loop outputs.
YY2 = []; % Create variables to store current states of plant and controller x = x0; % initial plant state xmpc = mpcstate(mpcobj); % pointer to current controller state
Start simulation loop
for ct=0:round(Tstop/Ts) % Plant equations: output update y = C*x + D(:,2)*v(ct+1); % Store output signals YY2 = [YY2,y]; %#ok<*AGROW> % Compute MPC law. Extracts references r(t+1),r(t+2),...,r(t+p) and % measured disturbances v(t),v(t+1),...,v(t+p) for previewing. u = mpcmove(mpcobj,xmpc,y,r(ct+2:ct+p+1),v(ct+1:ct+p+1)); % Plant equations: state update x = Ad*x+Bd(:,1)*u+Bd(:,2)*v(ct+1); end
Plot results.
figure t = 0:Ts:Tstop; plot(t,r(1:length(t)),'c:',t,YY1,'r-',t,YY2,'bo'); xlabel('Time'); ylabel('Plant Output'); legend( ... {'Reference'; 'From sim command'; 'From mpcmove command'}, ... Location="SouthEast"); grid
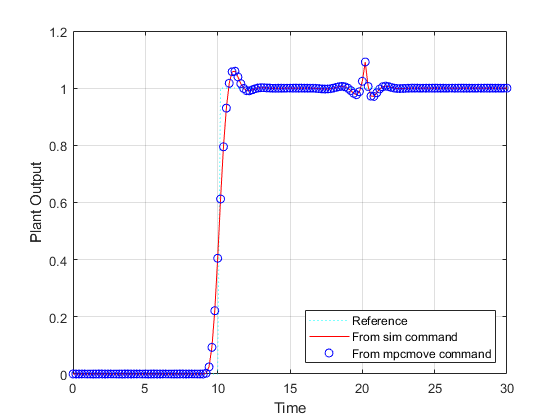
The responses are identical.
Optimal predicted trajectories are returned by mpcmove. Assume to you start from the current state and have a set-point change to 0.5 in 5 steps, and assume the measured disturbance has disappeared.
r1 = [ones(5,1);0.5*ones(p-5,1)]; v1 = zeros(p+1,1); [~,Info] = mpcmove(mpcobj,xmpc,y,r1(1:p),v1(1:p+1));
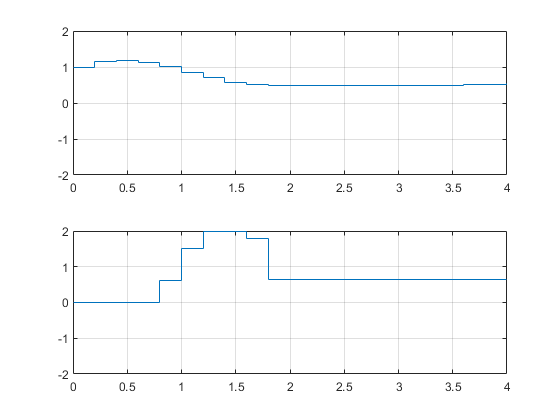
Extract the optimal predicted trajectories and plot them.
topt = Info.Topt; yopt = Info.Yopt; uopt = Info.Uopt; figure subplot(211) title('Optimal sequence of predicted outputs') stairs(topt,yopt); grid axis([0 p*Ts -2 2]); subplot(212) title('Optimal sequence of manipulated variables') stairs(topt,uopt); axis([0 p*Ts -2 2]); grid
Obtain LTI Representation of MPC Controller with Previewing
When the constraints are not active, the MPC controller behaves like a linear controller. You can get the state-space form of the MPC controller, with y, [r(t+1);r(t+2);...;r(t+p)], and [v(t);v(t+1);...;v(t+p)] as inputs to the controller.
Get state-space matrices of linearized controller.
LTI = ss(mpcobj,'rv','on','on'); [AL,BL,CL,DL] = ssdata(LTI);
Create array to store closed-loop outputs.
YY3 = [];
% Setup initial state of the MPC controller
x = x0;
xL = [x0;0;0];
Start main simulation loop
for ct=0:round(Tstop/Ts) % Plant output update y = Cd*x + Dd(:,2)*v(ct+1); % Save output and refs value YY3 =[YY3,y]; % Compute the linear MPC control action u = CL*xL + DL*[y;r(ct+2:ct+p+1);v(ct+1:ct+p+1)]; % Note that the optimal move provided by MPC would be: % mpcmove(mpcobj,xmpc,y,ref(t+2:t+p+1),v(t+1:t+p+1)); % Plant update x = Ad*x + Bd(:,1)*u + Bd(:,2)*v(ct+1); % Controller update xL = AL*xL + BL*[y;r(ct+2:ct+p+1);v(ct+1:ct+p+1)]; end
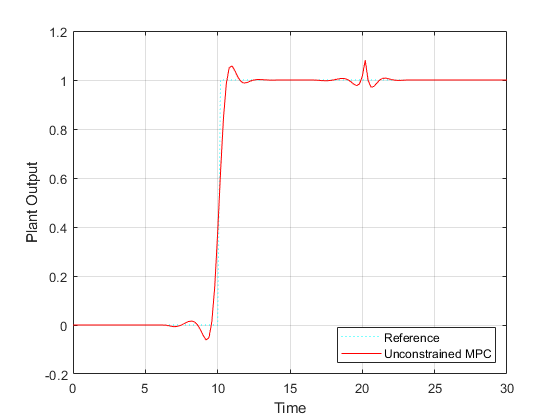
Plot results.
figure plot(t,r(1:length(t)),'c:',t,YY3,'r-'); xlabel('Time'); ylabel('Plant Output'); legend({'Reference';'Unconstrained MPC'},'Location','SouthEast'); grid
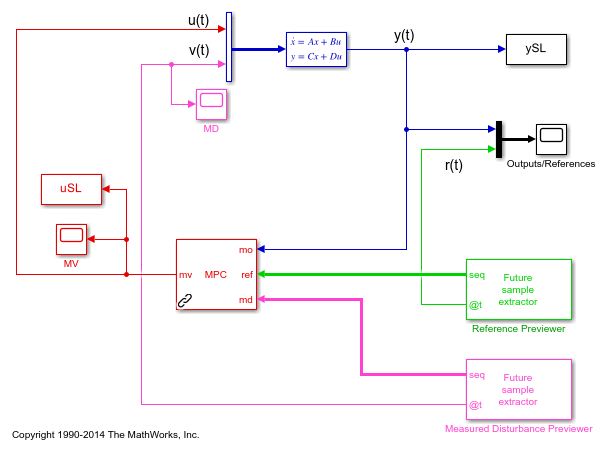
Simulate Using Simulink®
To run this example, Simulink® is required.
if ~mpcchecktoolboxinstalled('simulink') disp('Simulink(R) is required to run this example.') return end time = (0:Ts:(Tstop+p*Ts))'; % time vector r = double(time>10); % reference signal v = -double(time>20); % measured disturbance signal % Define the reference signal in structure ref.time = time; ref.signals.values = r; % Define the measured disturbance md.time = time; md.signals.values = v; % Open Simulink model mdl = 'mpc_preview'; open_system(mdl) % Simulate the model using the Simulink |sim| command sim(mdl,Tstop);
Plot results.
figure t = 0:Ts:Tstop; plot(t,r(1:length(t)),'c:',t,YY1,'r-',t,YY2,'bo',t,ySL,'gx'); xlabel('Time'); ylabel('Plant Output'); legend({'Reference'; ... 'From sim command'; ... 'From mpcmove command'; ... 'From Simulink'}, ... Location="SouthEast"); grid

The responses are identical.
See Also
Functions
mpcmove|mpcsimopt|mpcmoveopt|sim