Simulate Linear MPC Controller with Nonlinear Plant Using Successive Linearizations
Note
This example shows a no-longer-recommended way to simulate an MPC
controller in closed loop with a nonlinear plant in MATLAB®. The method is shown for illustrative purposes only, and relies on successive
linearizations of a Simulink® CSTR model and successive re-instantiations of an MPC controller object.
Recommended options to simulate an MPC controller with a nonlinear plant are discussed in
What Is Model Predictive Control?. To implement a successive
linearization approach in MATLAB, use mpcmoveAdaptive. For an example using
Simulink, see Adaptive MPC Control of Nonlinear Chemical Reactor Using Successive Linearization. For more detail, see Adaptive and Time-Varying MPC.
Control of a Linearized Plant Model
If your plant is a nonlinear Simulink model, you can linearize the plant (see Linearization Using Model Linearizer in Simulink Control Design) and design a controller for the linearized model (see Design MPC Controller in Simulink).
You then have several options to simulate the closed loop.
Using MPC Designer allows you to simulate the linear closed loop response while at the same time tuning the controller parameters.
Using MATLAB, you can simulate the linear closed loop using
sim, or you can simulate either the linear or nonlinear closed loop usingmpcmove. The first option is more straightforward but limited to linear plants and predetermined disturbance signals, while the second option allows for more flexibility in the choice of sampling strategy, plant, disturbance, and custom state estimation.Using Simulink, you can use the MPC Controller block (which takes your
mpcobject as a parameter) in closed loop with your plant model built in Simulink. This option allows for the greatest flexibility in simulating more complex systems and for easy generation of production code from your controller.
Often the plant to be controlled can be accurately approximated by a linear plant only locally, around a given operating point. This approximation might no longer be accurate as time passes and the plant operating point changes.
Control of the Nonlinear CSTR Model
The CSTR model described in CSTR Model is strongly nonlinear with respect to reactor temperature variations and can be open-loop unstable during the transition from one operating condition to another. As shown in Design MPC Controller in Simulink, a linear controller can regulate this plant, but degrades (and might even become unstable) if the operating point changes significantly.
You can still control the CSTR plant over a wide operating range using traditional MPC control techniques. To do so, you have a few options:
If a linear plant model cannot be obtained at run time, first you need to obtain several linear plant models offline at different operating conditions that cover the typical operating range. Next you can choose one of the two approaches to implement MPC control strategy:
(1) Design several MPC controllers offline, one for each plant model. At run time, use
the Multiple MPC Controller block (in Simulink) or mpcmoveMultiple (in MATLAB) to switch MPC controllers from one to another based on a desired scheduling
strategy. For more details, see Gain-Scheduled MPC Control of Nonlinear Chemical Reactor. Use this approach when the plant models have different
orders or time delays.
(2) Design one MPC controller offline at the initial operating point. At run time, use
the Adaptive MPC Controller block (in Simulink) or mpcmoveAdaptive (in MATLAB) to update the predictive model at each control interval. The Linear Parameter
Varying (LPV) System block can supply linear plant models with a given scheduling strategy,
given some input scheduling parameters. See Adaptive MPC Control of Nonlinear Chemical Reactor Using Linear Parameter-Varying System for more details. Use this
approach when all the plant models have the same order and time delay.
If a linear plant model with a fixed order and time delay can be obtained at run time, you should use the Adaptive MPC Controller block (in Simulink) or
mpcmoveAdaptive(in MATLAB) to achieve nonlinear control. There are two typical ways to obtain a linear plant model online:
(1) Use successive linearizations when a nonlinear plant model is available and can be
linearized at run time. This example shows an old method to perform successive linearization
while simulating the CSTR in MATLAB. This approach is no longer recommended, and is only
shown for comparison purposes. Use Adaptive MPC and mpcmoveAdaptive instead. Among other benefits, with Adaptive MPC you can
define an MPC controller only once at the beginning and update it at run time, thereby
avoiding to redefine of a linear MPC controller from scratch at each time step, as in the
following example. See Adaptive and Time-Varying MPC for more details. For an example on how to implement
Adaptive MPC in Simulink using the successive linearization approach, see Adaptive MPC Control of Nonlinear Chemical Reactor Using Successive Linearization.
(2) Use online estimation to identify a linear model in closed loop. See Adaptive MPC Control of Nonlinear Chemical Reactor Using Online Model Estimation for more details. Use this approach when a linear plant model cannot be obtained from either an LPV system or from successive linearization.
The entire range of options to control a nonlinear plant, including Nonlinear MPC, is discussed in What Is Model Predictive Control?.
Example Code for Successive Linearization
The objective of this example is to redefine the predictive controller at the beginning of each control interval so that its predictive model, though linear, represents the latest plant conditions as accurately as possible. This will be done by linearizing the nonlinear model repeatedly, allowing the controller to adapt as plant conditions change. For more details on this approach, see [1] and [2].
In the following code, the simulation begins at the nominal operating point of the
CSTR model (concentration = 8.57) and moves to a lower point
(concentration = 2) where the reaction rate is much higher. The required code is as
follows:
% Get initial states from simulink model [sys, xp] = CSTR_INOUT([],[],[],'sizes'); % Set initial inputs up = [10 298.15 298.15]; u = up(3); % coolant temperature = control input % Define storage arrays tsave = []; usave = []; ysave = []; rsave = []; % Define Sample time Ts = 1; % Simulation loop t = 0; while t < 40 % Assume plant output equal to plant state yp = xp; % Linearize the plant model at the current conditions [a,b,c,d] = linmod('CSTR_INOUT',xp,up); % Create MPC internal model Plant = ss(a,b,c,d); Plant.InputGroup.ManipulatedVariables = 3; Plant.InputGroup.UnmeasuredDisturbances = [1 2]; Model.Plant = Plant; % Set nominal conditions to the latest values Model.Nominal.U = [0 0 u]; Model.Nominal.X = xp; Model.Nominal.Y = yp; % dt = 1/1000th of control interval dt = 0.001; % set up simOptions simOptions.StartTime = num2str(t); simOptions.StopTime = num2str(t+dt); simOptions.LoadInitialState = 'on'; simOptions.InitialState = 'xp'; simOptions.SaveTime = 'on'; simOptions.SaveState = 'on'; simOptions.LoadExternalInput = 'on'; simOptions.ExternalInput = '[t up; t+dt up]'; % Simulate open loop Simulink CSTR model for 1/1000th % of control interval while maintaining fixed input simOut = sim('CSTR_INOUT',simOptions); % Collect open loop simulation outputs T = simOut.get('tout'); XP = simOut.get('xout'); YP = simOut.get('yout'); % Get nominal value of dxp/dt Model.Nominal.DX = (1/dt)*(XP(end,:)' - xp(:)); % Define MPC controller for the latest model mpcobj = mpc(Model, Ts); mpcobj.W.Output = [0 1]; % Define setpoint as a ramp signal r = max([8.57 - 0.25*t, 2]); % At the beginning of the simulation, get a % pointer to the state of the MPC controller if t <= 0 xd = [0; 0]; x = mpcstate(mpcobj,xp,xd,[],u); end % Calculate control action u = mpcmove(mpcobj,x,yp,[0 r],[]); % Set plant input to control action up(3) = u; % Set up simulation options simOptions.StartTime = num2str(t); simOptions.StopTime = num2str(t+Ts); simOptions.InitialState = 'xp'; simOptions.ExternalInput = '[t up; t+Ts up]'; % Simulate the plant for one control interval simOut = sim('CSTR_INOUT',simOptions); % Collect simulation outputs T = simOut.get('tout'); XP = simOut.get('xout'); YP = simOut.get('yout'); % Save results for plotting tsave = [tsave; T]; ysave = [ysave; YP]; usave = [usave; up(ones(length(T),1),:)]; rsave = [rsave; r(ones(length(T),1),:)]; % Update plant state xp = XP(end,:)'; % Update time t = t + Ts; end % Plot residual concentration figure(1) plot(tsave,[ysave(:,2) rsave]) title('Residual Concentration') % Plot coolant temperature figure(2) plot(tsave,usave(:,3)) title('Coolant Temperature')
CSTR Results and Discussion
The plotted results appear below. Note the following points:
The setpoint is being ramped from the initial concentration to the desired final value (see the step-wise changes in the reactor concentration plot below). The reactor concentration tracks this ramp smoothly with some delay (see the smooth curve), and settles at the final state with negligible overshoot. The controller works equally well (and achieves the final concentration more rapidly) for a step-wise setpoint change, but it makes unrealistically rapid changes in coolant temperature (not shown).
The final steady state requires a coolant temperature of 305.20 K (see the coolant temperature plot below). An interesting feature of this nonlinear plant is that if one starts at the initial steady state (coolant temperature = 298.15 K), stepping the coolant temperature to 305.20 and holding will not achieve the desired final concentration of 2. In fact, under this simple strategy the reactor concentration stabilizes at a final value of 7.88, far from the desired value. A successful controller must increase the reactor temperature until the reaction "takes off," after which it must reduce the coolant temperature to handle the increased heat load. The relinearization approach provides such a controller (see following plots).
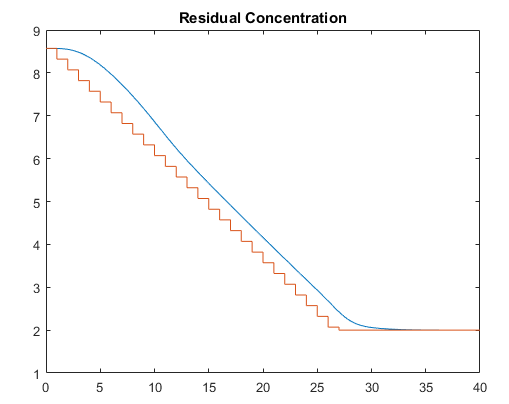
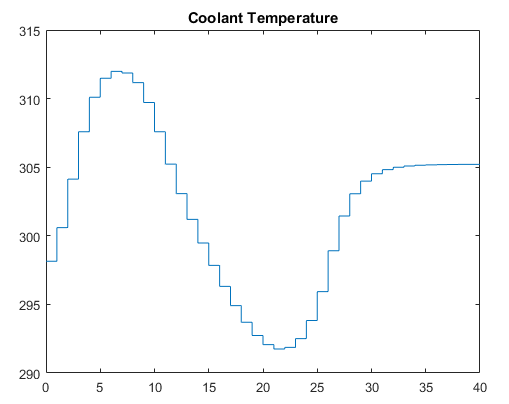
linmod(Simulink) relinearizes the plant as its state evolves. In general,linearizeis preferred. See also Linearization Using MATLAB Code and Linearize Nonlinear Models (Simulink Control Design).The code also resets the linear model's nominal conditions to the latest values. Note, however, that the first two input signals, which are unmeasured disturbances in the controller design, always have nominal zero values. As they are unmeasured, the controller cannot be informed of the true values. A non-zero value would cause an error.
Prior to defining a new MPC controller,
simis used to simulate the plant for a small fraction of the control interval. This is done to calculate, numerically, the nominal value of the time derivative of the plant state, at the current operating point.Function
mpcdefines a new controller based on the relinearized plant model. The output weight tuning ignores the temperature measurement, focusing only on the concentration.At t = 0, the
mpcstatefunction gets an handle to the initial extended state vector of the controller,x. Thereafter, thempcmovefunction updates the controller state automatically using the controller's default state estimator. It would also be possible to use an Extended Kalman Filter (EKF) as described in [1] and [2], in which case the EKF would reset thempcstateinput variables at each step.The
mpcmovefunction uses the latest controller definition and state, the measured plant outputs, and the setpoints to calculate the new coolant temperature at each step.The Simulink
simfunction simulates the nonlinear plant from the beginning to the end of the control interval. The final condition from the previous step is being used as the initial plant state, and that the plant inputs are being held constant during each interval.
Remember that a conventional feedback controller or a fixed Model Predictive Control Toolbox™ controller tuned to operate at the initial condition would become unstable as the plant moves to the final condition. Periodic model updating overcomes this problem automatically and provides excellent control under all conditions.
References
[1] Lee, J. H. and N. L. Ricker, "Extended Kalman Filter Based Nonlinear Model Predictive Control," Ind. Eng. Chem. Res., Vol. 33, No. 6, pp. 1530–1541 (1994).
[2] Ricker, N. L., and J. H. Lee "Nonlinear Model Predictive Control of the Tennessee Eastman Challenge Process," Computers & Chemical Engineering, Vol. 19, No. 9, pp. 961–981 (1995).
See Also
Functions
Objects
mpc|mpcstate|mpcmoveopt
Blocks
Topics
- CSTR Model
- Adaptive MPC Control of Nonlinear Chemical Reactor Using Successive Linearization
- Adaptive MPC Control of Nonlinear Chemical Reactor Using Linear Parameter-Varying System
- Adaptive MPC Control of Nonlinear Chemical Reactor Using Online Model Estimation
- What Is Model Predictive Control?
- Adaptive and Time-Varying MPC
- Gain-Scheduled MPC