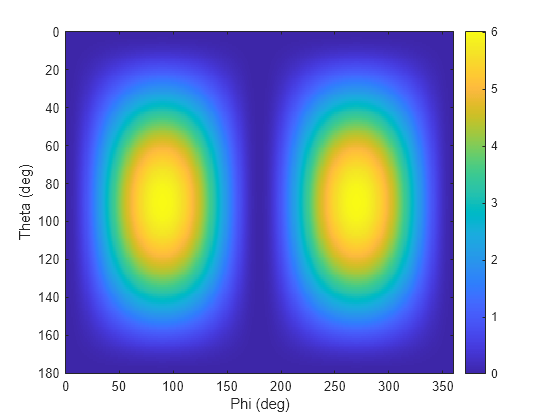azel2phithetapat
Convert radiation pattern from azimuth-elevation coordinates to phi-theta coordinates
Syntax
Description
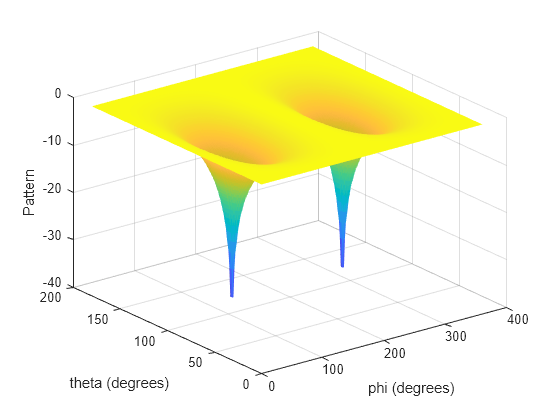
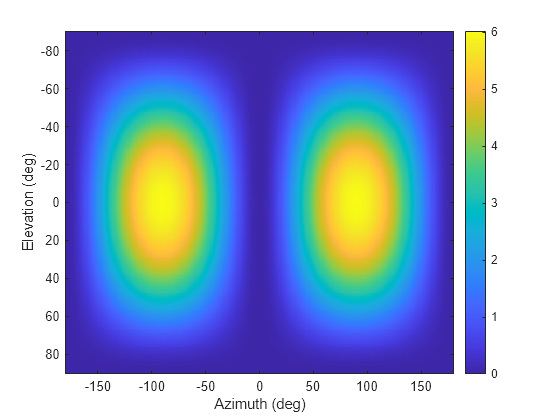
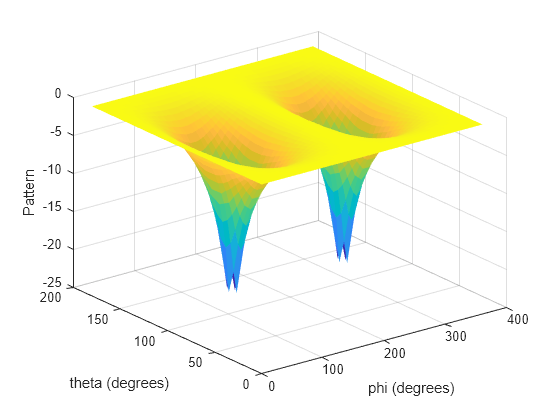
pat_phitheta = azel2phithetapat(pat_azel,az,el)pat_azel, from azimuth and
elevation coordinates to the pattern, pat_phitheta, in phi and theta
coordinates. az and el are the azimuth and
elevation angles at which the pat_azel values are defined. The
pat_phitheta matrix covers theta values from 0 to 180 degrees and phi
values from 0 to 360 degrees in one degree increments. The function interpolates the
pat_azel matrix to estimate the response of the antenna in a given
phi-theta direction.
pat_phitheta = azel2phithetapat(___,'RotateZ2X',rotpatax)rotpatax to indicate the boresight direction of the
pattern along the x-axis or the z-axis.
[
also returns vectors pat_phitheta,phi_pat,theta_pat] = azel2phithetapat(___)phi_pat and theta_pat
containing the phi and theta angles at which pat_phitheta is
sampled.
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2012a