pattern
Syntax
Description
pattern(___, plots the
array pattern with additional options specified by one or more
Name=Value)Name=Value pair arguments.
[
returns the array pattern in PAT,AZ_ANG,EL_ANG] = pattern(___)PAT. The AZ_ANG
output contains the coordinate values corresponding to the rows of PAT.
The EL_ANG output contains the coordinate values corresponding to the
columns of PAT. If the 'CoordinateSystem' parameter
is set to 'uv', then AZ_ANG contains the
U coordinates of the pattern and EL_ANG contains
the V coordinates of the pattern. Otherwise, they are in angular units in
degrees. UV units are dimensionless.
Note
When you need to compute array or element directivity, you can either set the
Type property to "directivity" in the
pattern object function or use the directivity
object function. For a small number of angular directions, it may be more computationally
efficient to use the directivity object function. The
pattern object function is more efficient for computing directivity
for larger angular regions.
Examples
Construct a 5G antenna array where the grid is 2-by-2 and each panel is a 4-by-4 array. Each antenna element consists of two short-dipole antennas with different dipole axis directions. The antenna elements are spaced 1/2 wavelength apart and the panels are spaced 3 wavelengths apart. Plot the response pattern of the array assuming an operating frequency of 6 GHz.
c = physconst('LightSpeed'); fc = 6e9; lambda = c/fc; antenna1 = phased.ShortDipoleAntennaElement(AxisDirection="Z"); antenna2 = phased.ShortDipoleAntennaElement(AxisDirection="X"); array = phased.NRRectangularPanelArray('ElementSet', ... {antenna1, antenna2},'Size',[4, 4, 2, 2],'Spacing', ... [0.5*lambda, 0.5*lambda,3*lambda, 3*lambda]); pattern(array,fc,ShowArray=true)

Use the Orientation property of pattern to change the orientation along the x-axis, along the y-axis and along the z-axis.
pattern(array,fc,Orientation=[80;30;60],ShowArray=true)

Disable the display of local coordinates and the colorbar.
pattern(array,fc,ShowLocalCoordinate=false,ShowColorBar=false)
Input Arguments
Phased array, specified as a Phased Array System Toolbox System object.
Frequencies for computing directivity and patterns, specified as a positive scalar or 1-by-L real-valued row vector. Frequency units are in hertz.
For an antenna, microphone, or sonar hydrophone or projector element,
FREQmust lie within the range of values specified by theFrequencyRangeorFrequencyVectorproperty of the element. Otherwise, the element produces no response and the directivity is returned as–Inf. Most elements use theFrequencyRangeproperty except forphased.CustomAntennaElementandphased.CustomMicrophoneElement, which use theFrequencyVectorproperty.For an array of elements,
FREQmust lie within the frequency range of the elements that make up the array. Otherwise, the array produces no response and the directivity is returned as–Inf.
Example: [1e8 2e6]
Data Types: double
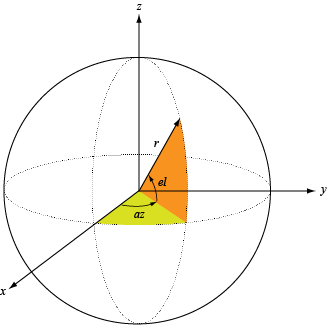
Azimuth angles for computing directivity and pattern, specified as a 1-by-N real-valued row vector where N is the number of azimuth angles. Angle units are in degrees. Azimuth angles must lie between –180° and 180°.
The azimuth angle is the angle between the x-axis and the projection of the direction vector onto the xy plane. When measured from the x-axis toward the y-axis, this angle is positive.
Example: [-45:2:45]
Data Types: double
Elevation angles for computing directivity and pattern, specified as a 1-by-M real-valued row vector where M is the number of desired elevation directions. Angle units are in degrees. The elevation angle must lie between –90° and 90°.
The elevation angle is the angle between the direction vector and xy-plane. The elevation angle is positive when measured towards the z-axis.
Example: [-75:1:70]
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: CoordinateSystem="polar",Type="directivity"
Plotting coordinate system of the pattern, specified as the comma-separated pair consisting of
CoordinateSystem and one of "polar",
"rectangular", or "uv". When
CoordinateSystem is set to "polar" or
"rectangular", the AZ and
EL arguments specify the pattern azimuth and elevation,
respectively. AZ values must lie between –180° and 180°.
EL values must lie between –90° and 90°. If
CoordinateSystem is set to "uv",
AZ and EL then specify
U and V coordinates, respectively.
AZ and EL must lie between -1 and
1.
Example: "uv"
Data Types: char
Displayed pattern type, specified as the equal-sign-separated pair consisting of
Type and one of
"directivity"— directivity pattern measured in dBi."efield"— field pattern of the sensor or array. For acoustic sensors, the displayed pattern is for the scalar sound field."power"— power pattern of the sensor or array defined as the square of the field pattern."powerdb"— power pattern converted to dB.
Example: "powerdb"
Data Types: char
Array orientation, specified as a 3-by-1 real-valued column vector containing three rotation angles. The three angles define orthogonal rotations with respect to the x-, y-, and z-axes of the local coordinate system. To create the full orientation matrix, the orthogonal rotations are applied in this order:
a rotation around the positive x-axis by the angle θx.
a rotation around the positive y-axis by the angle θy.
a rotation around the positive z-axis by the angle θz.
Positive angles are defined using the right-handed rule. A positive angle defines a rotation that appears clockwise when looking towards the positive direction of the axis, and negative values when the rotation appears counter-clockwise. The right-hand rule is invoked by pointing the right-hand thumb along an axis. Then the other fingers of the right hand curl in the positive direction,
Display normalized pattern, specified as the comma-separated pair consisting of
Normalize and a Boolean. Set this parameter to
true to display a normalized pattern. This parameter does not
apply when you set Type to "directivity".
Directivity patterns are already normalized.
Data Types: logical
View the array geometry along with the 3D radiation pattern, specified as
false or true.
Data Types: logical
Show the local coordinate axes, specified as true or false.
Data Types: logical
Show the colorbar, specified as true or false.
Data Types: logical
Handle to the axes along which the array geometry is displayed specified as a scalar.
Polarization type, specified as the comma-separated pair consisting of
Polarization and either "combined",
"H", or "V". If
Polarization is "combined", the horizontal
and vertical polarization patterns are combined. If Polarization
is "H", only the horizontal polarization is displayed. If
Polarization is "V", only the vertical
polarization is displayed.
Dependencies
To enable this property, set the array argument to an array
that supports polarization and then set the Type name-value pair
to "efield", "power", or
"powerdb".
Data Types: char | string
Signal propagation speed, specified as the comma-separated pair consisting of
PropagationSpeed and a positive scalar in meters per
second.
Example: PropagationSpeed="physconst('LightSpeed')"
Data Types: double
Array weights, specified as the comma-separated pair consisting
of 'Weights' and an N-by-1 complex-valued
column vector or N-by-L complex-valued
matrix. Array weights are applied to the elements of the array to
produce array steering, tapering, or both. The dimension N is
the number of elements in the array. The dimension L is
the number of frequencies specified by FREQ.
| Weights Dimension | FREQ Dimension | Purpose |
|---|---|---|
| N-by-1 complex-valued column vector | Scalar or 1-by-L row vector | Applies a set of weights for the single frequency or for all L frequencies. |
| N-by-L complex-valued matrix | 1-by-L row vector | Applies each of the L columns of 'Weights' for
the corresponding frequency in FREQ. |
Note
Use complex weights to steer the array response toward different
directions. You can create weights using the phased.SteeringVector System object or
you can compute your own weights. In general, you apply Hermitian
conjugation before using weights in any Phased Array System Toolbox function
or System object such as phased.Radiator or phased.Collector. However, for the directivity, pattern, patternAzimuth,
and patternElevation methods of any array System object use
the steering vector without conjugation.
Example: 'Weights',ones(N,M)
Data Types: double
Complex Number Support: Yes
Weights applied to each subarray element, specified as a NSE-by-N matrix or a cell array. When a matrix, NSE is the number of elements in each individual subarray and N is the number of subarrays. Each column in ElementWeights specifies the weights for the elements in the corresponding subarray.
Dependencies
To enable this parameter, set the SubarraySteering property of the array
to "Custom".
Data Types: double | cell
Complex Number Support: Yes
Output Arguments
More About
Directivity describes the directionality of the radiation pattern of a sensor element or array of sensor elements.
Higher directivity is desired when you want to transmit more radiation in a specific direction. Directivity is the ratio of the transmitted radiant intensity in a specified direction to the radiant intensity transmitted by an isotropic radiator with the same total transmitted power
where Urad(θ,φ) is the radiant intensity of a transmitter in the direction (θ,φ) and Ptotal is the total power transmitted by an isotropic radiator. For a receiving element or array, directivity measures the sensitivity toward radiation arriving from a specific direction. The principle of reciprocity shows that the directivity of an element or array used for reception equals the directivity of the same element or array used for transmission. When converted to decibels, the directivity is denoted as dBi. For information on directivity, read the notes on Element Directivity and Array Directivity.
Define the azimuth and elevation conventions used in the toolbox.
The azimuth angle of a vector is the angle between the x-axis and its orthogonal projection onto the xy-plane. The angle is positive when going from the x-axis toward the y-axis. Azimuth angles lie between –180° and 180° degrees, inclusive. The elevation angle is the angle between the vector and its orthogonal projection onto the xy-plane. The angle is positive when going toward the positive z-axis from the xy-plane. Elevation angles lie between –90° and 90° degrees, inclusive.
Version History
Introduced in R2023b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)