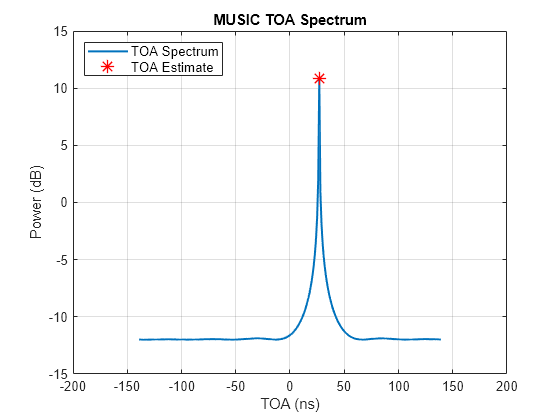
toaposest
Syntax
Description
Examples
Input Arguments
Output Arguments
Algorithms
References
[1] Zekavat, Seyed A., and R. Michael Buehrer, eds. Handbook of Position Location: Theory, Practice, and Advances. IEEE Series on Mobile & Digital Communication. Hoboken, New Jersey: Wiley-IEEE Press, 2019.
[2] Molisch, Andreas F. Wireless Communications: From Fundamentals to Beyond 5G. Third edition. IEEE Press. Hoboken, NJ: Wiley-IEEE Press, 2023.
[3] Chan, Y.T., and K.C. Ho. “A Simple and Efficient Estimator for Hyperbolic Location.” IEEE Transactions on Signal Processing 42, no. 8 (August 1994): 1905–15. https://doi.org/10.1109/78.301830.
[4] Stoica, P., and Arye Nehorai. “MUSIC, Maximum Likelihood, and Cramer-Rao Bound.” IEEE Transactions on Acoustics, Speech, and Signal Processing 37, no. 5 (May 1989): 720–41. https://doi.org/10.1109/29.17564.
Extended Capabilities
Version History
Introduced in R2024a