predict
Predict responses for new observations from linear incremental learning model
Syntax
Description
[ also returns classification scores for all classes when label,score] = predict(___)Mdl is an incremental learning model for classification, using any of the input argument combinations in the previous syntaxes.
Examples
Load the human activity data set.
load humanactivityFor details on the data set, enter Description at the command line.
Responses can be one of five classes: Sitting, Standing, Walking, Running, or Dancing. Dichotomize the response by identifying whether the subject is moving (actid > 2).
Y = actid > 2;
Fit a linear classification model to the entire data set.
TTMdl = fitclinear(feat,Y)
TTMdl =
ClassificationLinear
ResponseName: 'Y'
ClassNames: [0 1]
ScoreTransform: 'none'
Beta: [60×1 double]
Bias: -0.2005
Lambda: 4.1537e-05
Learner: 'svm'
Properties, Methods
TTMdl is a ClassificationLinear model object representing a traditionally trained linear classification model.
Convert the traditionally trained linear classification model to a binary classification linear model for incremental learning.
IncrementalMdl = incrementalLearner(TTMdl)
IncrementalMdl =
incrementalClassificationLinear
IsWarm: 1
Metrics: [1×2 table]
ClassNames: [0 1]
ScoreTransform: 'none'
Beta: [60×1 double]
Bias: -0.2005
Learner: 'svm'
Properties, Methods
IncrementalMdl is an incrementalClassificationLinear model object prepared for incremental learning using SVM.
The
incrementalLearnerfunction initializes the incremental learner by passing learned coefficients to it, along with other informationTTMdllearned from the training data.IncrementalMdlis warm (IsWarmis1), which means that incremental learning functions can start tracking performance metrics.The
incrementalLearnerconfigures the model to be trained using the adaptive scale-invariant solver, whereasfitclineartrainedTTMdlusing the BFGS solver.
An incremental learner created from converting a traditionally trained model can generate predictions without further processing.
Predict class labels for all observations using both models.
ttlabels = predict(TTMdl,feat); illables = predict(IncrementalMdl,feat); sameLabels = sum(ttlabels ~= illables) == 0
sameLabels = logical
1
Both models predict the same labels for each observation.
If you orient the observations along the columns of the predictor data matrix, you can experience an efficiency boost during incremental learning.
Load and shuffle the 2015 NYC housing data set. For more details on the data, see NYC Open Data.
load NYCHousing2015 rng(1) % For reproducibility n = size(NYCHousing2015,1); shuffidx = randsample(n,n); NYCHousing2015 = NYCHousing2015(shuffidx,:);
Extract the response variable SALEPRICE from the table. Apply the log transform to SALEPRICE.
Y = log(NYCHousing2015.SALEPRICE + 1); % Add 1 to avoid log of 0
NYCHousing2015.SALEPRICE = [];Create dummy variable matrices from the categorical predictors.
catvars = ["BOROUGH" "BUILDINGCLASSCATEGORY" "NEIGHBORHOOD"]; dumvarstbl = varfun(@(x)dummyvar(categorical(x)),NYCHousing2015,... 'InputVariables',catvars); dumvarmat = table2array(dumvarstbl); NYCHousing2015(:,catvars) = [];
Treat all other numeric variables in the table as linear predictors of sales price. Concatenate the matrix of dummy variables to the rest of the predictor data, and transpose the data to speed up computations.
idxnum = varfun(@isnumeric,NYCHousing2015,'OutputFormat','uniform'); X = [dumvarmat NYCHousing2015{:,idxnum}]';
Configure a linear regression model for incremental learning with no estimation period.
Mdl = incrementalRegressionLinear('Learner','leastsquares','EstimationPeriod',0);
Mdl is an incrementalRegressionLinear model object.
Perform incremental learning and prediction by following this procedure for each iteration:
Simulate a data stream by processing a chunk of 100 observations at a time.
Fit the model to the incoming chunk of data. Specify that the observations are oriented along the columns of the data. Overwrite the previous incremental model with the new model.
Predict responses using the fitted model and the incoming chunk of data. Specify that the observations are oriented along the columns of the data.
% Preallocation numObsPerChunk = 100; n = numel(Y); nchunk = floor(n/numObsPerChunk); r = nan(n,1); figure h = plot(r); h.YDataSource = 'r'; ylabel('Residuals') xlabel('Iteration') % Incremental fitting for j = 2:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = fit(Mdl,X(:,idx),Y(idx),'ObservationsIn','columns'); yhat = predict(Mdl,X(:,idx),'ObservationsIn','columns'); r(idx) = Y(idx) - yhat; refreshdata drawnow end
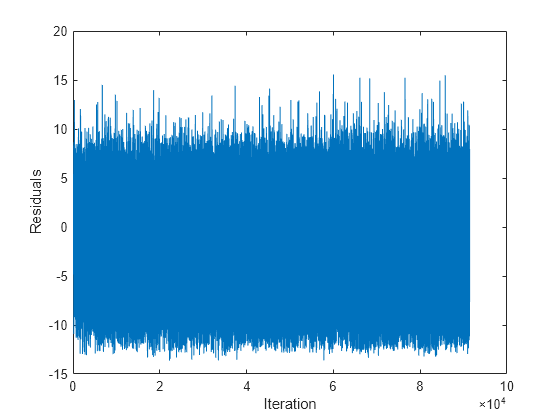
Mdl is an incrementalRegressionLinear model object trained on all the data in the stream.
The residuals appear symmetrically spread around 0 throughout incremental learning.
To compute posterior class probabilities, specify a logistic regression incremental learner.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(10); % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Responses can be one of five classes: Sitting, Standing, Walking, Running, or Dancing. Dichotomize the response by identifying whether the subject is moving (actid > 2).
Y = Y > 2;
Create an incremental logistic regression model for binary classification. Prepare it for predict by specifying the class names and arbitrary coefficient and bias values.
p = size(X,2); Beta = randn(p,1); Bias = randn(1); Mdl = incrementalClassificationLinear('Learner','logistic','Beta',Beta,... 'Bias',Bias,'ClassNames',unique(Y));
Mdl is an incrementalClassificationLinear model. All its properties are read-only. Instead of specifying arbitrary values, you can take either of these actions to prepare the model:
Train a logistic regression model for binary classification using
fitclinearon a subset of the data (if available), and then convert the model to an incremental learner by usingincrementalLearner.Incrementally fit
Mdlto data by usingfit.
Simulate a data stream, and perform the following actions on each incoming chunk of 50 observations.
Call
predictto predict classification scores for the observations in the incoming chunk of data. The classification scores are posterior class probabilities for logistic regression learners.Call
rocmetricsto compute the area under the ROC curve (AUC) using the incoming chunk of data, and store the result.Call
fitto fit the model to the incoming chunk. Overwrite the previous incremental model with a new one fitted to the incoming observations.
numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); auc = zeros(nchunk,1); % Incremental learning for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; [~,posteriorProb] = predict(Mdl,X(idx,:)); rocObj = rocmetrics(Y(idx),posteriorProb,Mdl.ClassNames); auc(j) = rocObj.AUC(1); Mdl = fit(Mdl,X(idx,:),Y(idx)); end
Mdl is an incrementalClassificationLinear model object trained on all the data in the stream.
Plot the AUC on the incoming chunks of data.
plot(auc) ylabel('AUC') xlabel('Iteration')

The plot suggests that the classifier predicts moving subjects well during incremental learning.
Input Arguments
Incremental learning model, specified as an incrementalClassificationLinear or incrementalRegressionLinear model object. You can create Mdl directly or by converting a supported, traditionally trained machine learning model using the incrementalLearner function. For more details, see the corresponding reference page.
You must configure Mdl to predict labels for a batch of observations.
If
Mdlis a converted, traditionally trained model, you can predict labels without any modifications.Otherwise,
Mdlmust satisfy the following criteria, which you can specify directly or by fittingMdlto data usingfitorupdateMetricsAndFit.If
Mdlis anincrementalRegressionLinearmodel, its model coefficientsMdl.Betaand biasMdl.Biasmust be nonempty arrays.If
Mdlis anincrementalClassificationLinearmodel, its model coefficientsMdl.Betaand biasMdl.Biasmust be nonempty arrays and the class names inMdl.ClassNamesmust contain two classes.Regardless of object type, if you configure the model so that functions standardize predictor data, the predictor means
Mdl.Muand standard deviationsMdl.Sigmamust be nonempty arrays.
Batch of predictor data for which to predict labels, specified as a floating-point matrix of n observations and Mdl.NumPredictors predictor variables. The value of dimension determines the orientation of the variables and observations.
Note
predict supports only floating-point
input predictor data. If your input data includes categorical data, you must prepare an encoded
version of the categorical data. Use dummyvar to convert each categorical variable
to a numeric matrix of dummy variables. Then, concatenate all dummy variable matrices and any
other numeric predictors. For more details, see Dummy Variables.
Data Types: single | double
Predictor data observation dimension, specified as 'columns' or 'rows'.
Example: 'ObservationsIn','columns'
Data Types: char | string
Output Arguments
Predicted responses (labels), returned as a categorical or character array;
floating-point, logical, or string vector; or cell array of character vectors with
n rows. n is the number of observations in
X, and label(
is the predicted response for observation
j)j
For regression problems,
labelis a floating-point vector.For classification problems,
labelhas the same data type as the class names stored inMdl.ClassNames. (The software treats string arrays as cell arrays of character vectors.)The
predictfunction classifies an observation into the class yielding the highest score. For an observation withNaNscores, the function classifies the observation into the majority class, which makes up the largest proportion of the training labels.
Classification scores, returned as an n-by-2 floating-point
matrix when Mdl is an
incrementalClassificationLinear model. n is the
number of observations in X.
score(
is the score for classifying observation j,k)jkMdl.ClassNames specifies the order of the classes.
If Mdl.Learner is 'svm',
predict returns raw classification scores. If
Mdl.Learner is 'logistic', classification scores
are posterior probabilities.
More About
For linear incremental learning models for binary classification, the raw classification score for classifying the observation x, a row vector, into the positive class is
where
β0 is the scalar bias
Mdl.Bias.β is the column vector of coefficients
Mdl.Beta.
The raw classification score for classifying x into the negative class is –f(x). The software classifies observations into the class that yields the positive score.
If the linear classification model consists of logistic regression learners, then the software applies the 'logit' score transformation to the raw classification scores.
Extended Capabilities
Usage notes and limitations:
Use
saveLearnerForCoder,loadLearnerForCoder, andcodegen(MATLAB Coder) to generate code for thepredictfunction. Save a trained model by usingsaveLearnerForCoder. Define an entry-point function that loads the saved model by usingloadLearnerForCoderand calls thepredictfunction. Then usecodegento generate code for the entry-point function.To generate single-precision C/C++ code for
predict, specifyDataType="single"when you call theloadLearnerForCoderfunction.This table contains notes about the arguments of
predict. Arguments not included in this table are fully supported.Argument Notes and Limitations MdlFor usage notes and limitations of the model object, see
incrementalClassificationLinearorincrementalRegressionLinear.XBatch-to-batch, the number of observations can be a variable size.
The number of predictor variables must equal to
Mdl.NumPredictors.Xmust besingleordouble.
The following restrictions apply:
If you configure
Mdlto shuffle data (Mdl.Shuffleistrue, orMdl.Solveris'sgd'or'asgd'), thepredictfunction randomly shuffles each incoming batch of observations before it fits the model to the batch. The order of the shuffled observations might not match the order generated by MATLAB®. Therefore, if you fitMdlbefore generating predictions, the predictions computed in MATLAB and those computed by the generated code might not be equal.Use a homogeneous data type for all floating-point input arguments and object properties, specifically, either
singleordouble.
For more information, see Introduction to Code Generation.
Version History
Introduced in R2020b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)