predict
Syntax
Description
predictedY = predict(Mdl,X)X using the trained quantile neural network regression model
Mdl.
predictedY = predict(Mdl,X,Name=Value)
[
additionally returns a vector predictedY,crossingIndicator] = predict(___)crossingIndicator whose entries indicate
whether predictions for the specified quantiles cross each other.
Examples
Fit a quantile neural network regression model using the 0.25, 0.50, and 0.75 quantiles.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a matrix X containing the predictor variables Acceleration, Displacement, Horsepower, and Weight. Store the response variable MPG in the variable Y.
load carbig
X = [Acceleration,Displacement,Horsepower,Weight];
Y = MPG;Delete rows of X and Y where either array has missing values.
R = rmmissing([X Y]); X = R(:,1:end-1); Y = R(:,end);
Partition the data into training data (XTrain and YTrain) and test data (XTest and YTest). Reserve approximately 20% of the observations for testing, and use the rest of the observations for training.
rng(0,"twister") % For reproducibility of the partition c = cvpartition(length(Y),"Holdout",0.20); trainingIdx = training(c); XTrain = X(trainingIdx,:); YTrain = Y(trainingIdx); testIdx = test(c); XTest = X(testIdx,:); YTest = Y(testIdx);
Train a quantile neural network regression model. Specify to use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, standardize the numeric predictors. Use a ridge (L2) regularization term of 1. Adding a regularization term can help prevent quantile crossing.
Mdl = fitrqnet(XTrain,YTrain,Quantiles=[0.25,0.50,0.75], ...
Standardize=true,Lambda=0.05)Mdl =
RegressionQuantileNeuralNetwork
ResponseName: 'Y'
CategoricalPredictors: []
LayerSizes: 10
Activations: 'relu'
OutputLayerActivation: 'none'
Quantiles: [0.2500 0.5000 0.7500]
Properties, Methods
Mdl is a RegressionQuantileNeuralNetwork model object. You can use dot notation to access the properties of Mdl. For example, Mdl.LayerWeights and Mdl.LayerBiases contain the weights and biases, respectively, for the fully connected layers of the trained model.
In this example, you can use the layer weights, layer biases, predictor means, and predictor standard deviations directly to predict the test set responses for each of the three quantiles in Mdl.Quantiles. In general, you can use the predict object function to make quantile predictions.
firstFCStep = (Mdl.LayerWeights{1})*((XTest-Mdl.Mu)./Mdl.Sigma)' ...
+ Mdl.LayerBiases{1};
reluStep = max(firstFCStep,0);
finalFCStep = (Mdl.LayerWeights{end})*reluStep + Mdl.LayerBiases{end};
predictedY = finalFCStep'predictedY = 78×3
13.9602 15.1340 16.6884
11.2792 12.2332 13.4849
19.5525 21.7303 23.9473
22.6950 25.5260 28.1201
10.4533 11.3377 12.4984
17.6935 19.5194 21.5152
12.4312 13.4797 14.8614
11.7998 12.7963 14.1071
16.6860 18.3305 20.2070
24.1142 27.0301 29.7811
22.2832 25.1327 27.6841
12.8749 13.9594 15.3917
12.2328 13.2643 14.6245
24.0164 26.9150 29.6545
13.4641 14.5970 16.0957
⋮
isequal(predictedY,predict(Mdl,XTest))
ans = logical
1
Each column of predictedY corresponds to a separate quantile (0.25, 0.5, or 0.75).
Visualize the predictions of the quantile neural network regression model. First, create a grid of predictor values.
minX = floor(min(X))
minX = 1×4
8 68 46 1613
maxX = ceil(max(X))
maxX = 1×4
25 455 230 5140
gridX = zeros(100,size(X,2)); for p = 1:size(X,2) gridp = linspace(minX(p),maxX(p))'; gridX(:,p) = gridp; end
Next, use the trained model Mdl to predict the response values for the grid of predictor values.
gridY = predict(Mdl,gridX)
gridY = 100×3
31.2419 35.0661 38.6357
30.8637 34.6317 38.1573
30.4854 34.1972 37.6789
30.1072 33.7627 37.2005
29.7290 33.3283 36.7221
29.3507 32.8938 36.2436
28.9725 32.4593 35.7652
28.5943 32.0249 35.2868
28.2160 31.5904 34.8084
27.8378 31.1560 34.3300
27.4596 30.7215 33.8516
27.0814 30.2870 33.3732
26.7031 29.8526 32.8948
26.3249 29.4181 32.4164
25.9467 28.9837 31.9380
⋮
For each observation in gridX, the predict object function returns predictions for the quantiles in Mdl.Quantiles.
View the gridY predictions for the second predictor (Displacement). Compare the quantile predictions to the true test data values.
predictorIdx = 2; plot(XTest(:,predictorIdx),YTest,".") hold on plot(gridX(:,predictorIdx),gridY(:,1)) plot(gridX(:,predictorIdx),gridY(:,2)) plot(gridX(:,predictorIdx),gridY(:,3)) hold off xlabel("Predictor (Displacement)") ylabel("Response (MPG)") legend(["True values","0.25 predicted values", ... "0.50 predicted values","0.75 predicted values"]) title("Test Data")
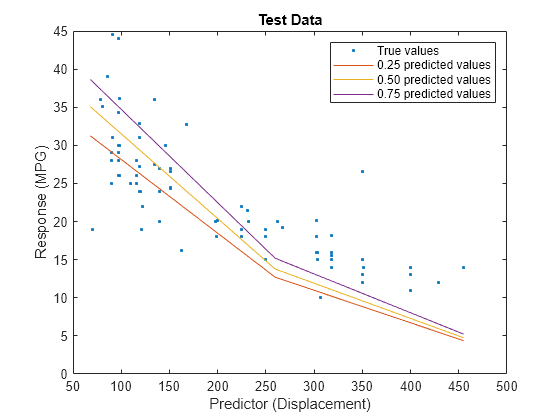
The red curve shows the predictions for the 0.25 quantile, the yellow curve shows the predictions for the 0.50 quantile, and the purple curve shows the predictions for the 0.75 quantile. The blue points indicate the true test data values.
Notice that the quantile prediction curves do not cross each other.
When training a quantile neural network regression model, you can use a ridge (L2) regularization term to prevent quantile crossing.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Cylinders, Displacement, and so on, as well as the response variable MPG.
load carbig cars = table(Acceleration,Cylinders,Displacement, ... Horsepower,Model_Year,Origin,Weight,MPG);
Remove rows of cars where the table has missing values.
cars = rmmissing(cars);
Categorize the cars based on whether they were made in the USA.
cars.Origin = categorical(cellstr(cars.Origin)); cars.Origin = mergecats(cars.Origin,["France","Japan",... "Germany","Sweden","Italy","England"],"NotUSA");
Partition the data into training and test sets using cvpartition. Use approximately 80% of the observations as training data, and 20% of the observations as test data.
rng(0,"twister") % For reproducibility of the data partition c = cvpartition(height(cars),"Holdout",0.20); trainingIdx = training(c); carsTrain = cars(trainingIdx,:); testIdx = test(c); carsTest = cars(testIdx,:);
Train a quantile neural network regression model. Use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, standardize the numeric predictors before training.
Mdl = fitrqnet(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ... Standardize=true);
Mdl is a RegressionNeuralNetwork model object.
Determine if the test data predictions for the quantiles in Mdl.Quantiles cross each other by using the predict object function of Mdl. The crossingIndicator output argument contains a value of 1 (true) for any observation with quantile predictions that cross.
[~,crossingIndicator] = predict(Mdl,carsTest); sum(crossingIndicator)
ans = 2
In this example, two of the observations in carsTest have quantile predictions that cross each other.
To prevent quantile crossing, specify the Lambda name-value argument in the call to fitrqnet. Use a 0.05 ridge (L2) penalty term.
newMdl = fitrqnet(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ... Standardize=true,Lambda=0.05); [predictedY,newCrossingIndicator] = predict(newMdl,carsTest); sum(newCrossingIndicator)
ans = 0
With regularization, the predictions for the test data set do not cross for any observations.
Visualize the predictions returned by newMdl by using a scatter plot with a reference line. Plot the predicted values along the vertical axis and the true response values along the horizontal axis. Points on the reference line indicate correct predictions.
plot(carsTest.MPG,predictedY(:,1),".") hold on plot(carsTest.MPG,predictedY(:,2),".") plot(carsTest.MPG,predictedY(:,3),".") plot(carsTest.MPG,carsTest.MPG) hold off xlabel("True MPG") ylabel("Predicted MPG") legend(["0.25 quantile values","0.50 quantile values", ... "0.75 quantile values","Reference line"], ... Location="southeast") title("Test Data")
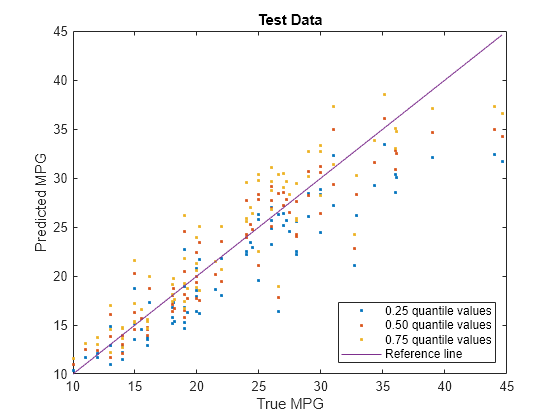
Blue points correspond to the 0.25 quantile, red points correspond to the 0.50 quantile, and yellow points correspond to the 0.75 quantile.
For a more in-depth example, see Regularize Quantile Regression Model to Prevent Quantile Crossing.
Input Arguments
Trained quantile neural network regression model, specified as a RegressionQuantileNeuralNetwork or CompactRegressionQuantileNeuralNetwork model object.
Predictor data, specified as a numeric matrix or a table. Unless you specify the
ObservationsIn name-value argument, each row of
X corresponds to one observation, and each column corresponds to
one variable.
For a numeric matrix:
The variables in
Xmust have the same order as the predictor variables that trainedMdl.If you train
Mdlusing a table (for example,Tbl) andTblcontains only numeric predictor variables, thenXcan be a numeric matrix. To treat numeric predictors inTblas categorical during training, identify categorical predictors by using theCategoricalPredictorsname-value argument offitrqnet. IfTblcontains heterogeneous predictor variables (for example, numeric and categorical data types) andXis a numeric matrix, thenpredictissues an error.
For a table:
predictdoes not support multicolumn variables or cell arrays other than cell arrays of character vectors.If you train
Mdlusing a table (for example,Tbl), then all predictor variables inXmust have the same variable names and data types as the variables that trainedMdl(stored inMdl.PredictorNames). However, the column order ofXdoes not need to correspond to the column order ofTbl. Also,TblandXcan contain additional variables (response variable, observation weights, and so on), butpredictignores them.If you train
Mdlusing a numeric matrix, then the predictor names inMdl.PredictorNamesmust be the same as the corresponding predictor variable names inX. To specify predictor names during training, use thePredictorNamesname-value argument offitrqnet. All predictor variables inXmust be numeric vectors.Xcan contain additional variables (response variable, observation weights, and so on), butpredictignores them.
If you set Standardize to true in
fitrqnet when training Mdl, then the
software standardizes the numeric columns of the predictor data using the corresponding
means (Mdl.Mu) and standard deviations
(Mdl.Sigma).
Note
If you orient your predictor matrix so that observations correspond to columns and
specify ObservationsIn="columns", then you might experience a
significant reduction in computation time. You cannot specify
ObservationsIn="columns" for predictor data in a table.
Data Types: single | double | table
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: predict(Mdl,X,ObservationsIn="columns") specifies that
columns in the predictor data correspond to observations.
Quantiles for which to compute predictions, specified as a vector of values in
Mdl.Quantiles. The predict function returns
predictions for each quantile.
Example: Quantiles=[0.4 0.6]
Data Types: single | double | char | string
Predictor data observation dimension, specified as "rows" or
"columns".
Note
If you orient your predictor matrix so that observations correspond to columns
and specify ObservationsIn="columns", then you might experience a
significant reduction in computation time. You cannot specify
ObservationsIn="columns" for predictor data in a table.
Example: ObservationsIn="columns"
Data Types: char | string
Since R2025a
Predicted response value to use for observations with missing predictor values,
specified as "quantile", a numeric scalar, or a numeric
vector.
| Value | Description |
|---|---|
"quantile" | predict uses the specified quantile of the
observed response values in the training data as the predicted response value
for observations with missing predictor values. |
| Numeric scalar or vector |
|
Example: PredictionForMissingValue=NaN
Data Types: single | double | char | string
Output Arguments
Quantile crossing indicator, returned as a logical vector. Each entry corresponds to
an observation in X. A value of 1
(true) indicates that the corresponding observation has predictions
that cross. That is, two quantiles q1 and q2 exist
in Quantiles such that q1 < q2
and predictedYq1
>
predictedYq2.
Version History
Introduced in R2024bYou can predict responses for a compact quantile regression model (CompactRegressionQuantileNeuralNetwork).
You can also specify the prediction values for observations with missing predictor
values by using the PredictionForMissingValues name-value argument. In previous releases,
observations with missing predictor values have NaN predictions. That is,
the behavior is equivalent to PredictionForMissingValue=NaN.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)