Create the following system of differential algebraic equations. Here, the symbolic functions x1(t), x2(t), and x3(t) represent state variables of the system. The system also contains symbolic parameters a and b.
eqs(t) =
Find the state variables of the system of equations. Often, these variables are functions of time only. To programmatically determine the state variables, use findSymType by specifying symfunOf as t.
Find the mass matrix form of this system.
F =
Next, assign the values of a and b as 2 and 1, respectively. Also, replace the state variables by variables Y1, Y2, and so on, that are acceptable by matlabFunction. You can use sym to programmatically generate the variables Y1, Y2, and so on.
Create the following function handles MM and FF. You use these function handles as input arguments for odeset and ode15s. These functions require state variables to be specified as column vectors. Because the symbolic variables in vecY are complex, use the nonconjugate transpose to convert vecY to a column vector.
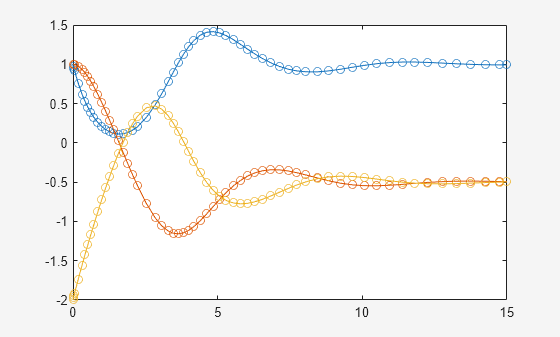
Solve the system using ode15s. Specify the initial values for the variables Y1, Y2, and Y3 as 1, 1, and -2, respectively. Plot the solutions over the time interval [0 15].