Wavelet Packets
The wavelet packet method is a generalization of wavelet decomposition that offers a richer signal analysis.
Wavelet packet atoms are waveforms indexed by three naturally interpreted parameters: position, scale (as in wavelet decomposition), and frequency.
For a given orthogonal wavelet function, we generate a library of bases called wavelet packet bases. Each of these bases offers a particular way of coding signals, preserving global energy, and reconstructing exact features. The wavelet packets can be used for numerous expansions of a given signal. We then select the most suitable decomposition of a given signal with respect to an entropy-based criterion.
There exist simple and efficient algorithms for both wavelet packet decomposition and optimal decomposition selection. We can then produce adaptive filtering algorithms with direct applications in optimal signal coding and data compression.
From Wavelets to Wavelet Packets
In the orthogonal wavelet decomposition procedure, the generic step splits the approximation coefficients into two parts. After splitting we obtain a vector of approximation coefficients and a vector of detail coefficients, both at a coarser scale. The information lost between two successive approximations is captured in the detail coefficients. Then the next step consists of splitting the new approximation coefficient vector; successive details are never reanalyzed.
In the corresponding wavelet packet situation, each detail coefficient vector is also decomposed into two parts using the same approach as in approximation vector splitting. This offers the richest analysis: the complete binary tree is produced as shown in the following figure.
Wavelet Packet Decomposition Tree at Level 3

The idea of this decomposition is to start from a scale-oriented decomposition, and then to analyze the obtained signals on frequency subbands.
Wavelet Packets in Action: An Introduction
This example illustrates certain differences between wavelet analysis and wavelet packet analysis.
Wavelet Packet Spectrum
The spectral analysis of wide-sense stationary signals using the Fourier transform is well-established. For nonstationary signals, there exist local Fourier methods such as the short-time Fourier transform (STFT). See Short-Time Fourier Transform for a brief description.
Because wavelets are localized in time and frequency, it is possible to use wavelet-based counterparts to the STFT for the time-frequency analysis of nonstationary signals. For example, it is possible to construct the scalogram based on the continuous wavelet transform (CWT). However, a potential drawback of using the CWT is that it is computationally expensive.
The discrete wavelet transform (DWT) permits a time-frequency decomposition of the input signal, but the degree of frequency resolution in the DWT is typically considered too coarse for practical time-frequency analysis.
As a compromise between the DWT- and CWT-based techniques, wavelet packets provide a computationally efficient alternative with sufficient frequency resolution. You can use wpspectrum to perform a time-frequency analysis of your signal using wavelet packets.
Local Spectral Analysis Using Wavelet Packets
The following examples illustrate the use of wavelet packets to perform a local spectral analysis. You use stft (Signal Processing Toolbox) as a benchmark to compare against the wavelet packet spectrum.
Sine Wave
Generate a sine wave with frequency 128 Hz. Sample the signal at 1 kHz.
Fs = 1e3; frq = 128; t = 0:1/Fs:2; sig = sin(2*pi*frq*t);
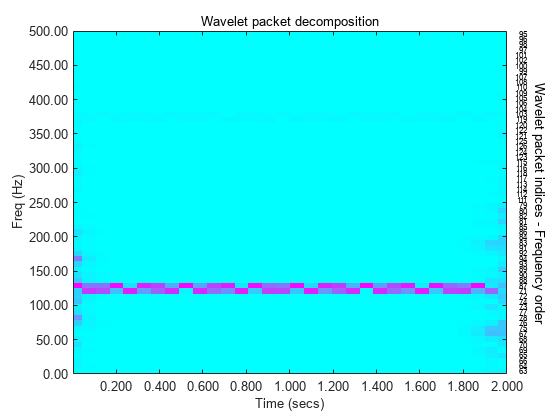
Use the wpdec function to obtain the wavelet packet decomposition of the signal down to level 6. Use the sym8 wavelet. Plot the magnitude of the wavelet packet power spectrum.
figure level = 6; wpt = wpdec(sig,level,"sym8"); [spec,tm,frq] = wpspectrum(wpt,Fs,"plot");
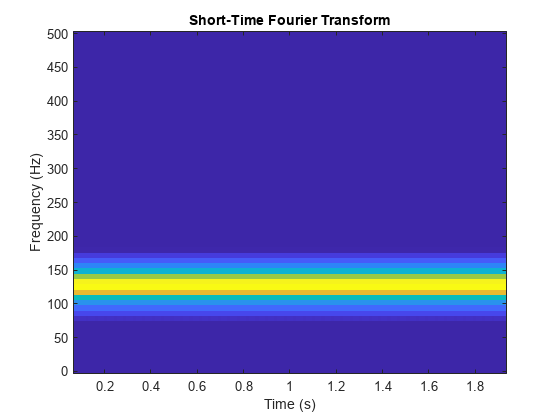
Compare with a plot of the magnitude of the STFT of the same signal.
windowsize = 128; window = hanning(windowsize); noverlap = windowsize-1; stft(sig,Fs,Window=window,OverlapLength=noverlap, ... FrequencyRange="onesided") colorbar off colormap("default")
Sum of Sine Waves
Generate the sum of two sine waves with frequencies 64 Hz and 128 Hz, respectively. Sample the signal at 1 kHz.
Fs = 1e3;
frq1 = 64;
frq2 = 128;
t = 0:1/Fs:2;
sig = sin(2*pi*frq1*t) + ...
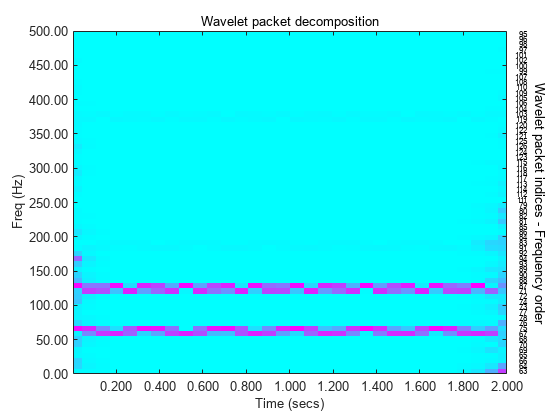
sin(2*pi*frq2*t);Plot the magnitude of the wavelet packet power spectrum.
clf wpt = wpdec(sig,level,"sym8"); [Spec,Time,Freq] = wpspectrum(wpt,Fs,"plot");
Compare with a plot of the magnitude of the STFT.
stft(sig,Fs,Window=window,OverlapLength=noverlap, ... FrequencyRange="onesided") colorbar off colormap("default")
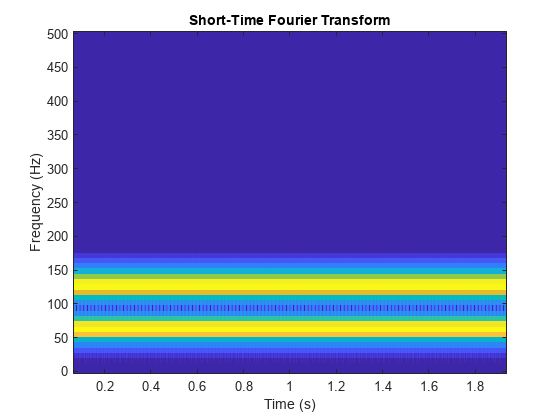
Abrupt Frequency Change
Generate a signal with an abrupt change in frequency from 16 Hz to 64 Hz at two seconds. Sample the signal at 500 Hz.
Fs = 500;
frq1 = 16;
frq2 = 64;
t = 0:1/Fs:4;
sig = sin(2*pi*frq1*t).*(t<2) + ...
sin(2*pi*frq2*t).*(t>=2);Plot the magnitude of the wavelet packet power spectrum.
clf wpt = wpdec(sig,level,"sym8"); [Spec,Time,Freq] = wpspectrum(wpt,Fs,"plot");

Compare with a plot of the magnitude of the STFT.
stft(sig,Fs,Window=window,OverlapLength=noverlap, ... FrequencyRange="onesided") colorbar off colormap("default")
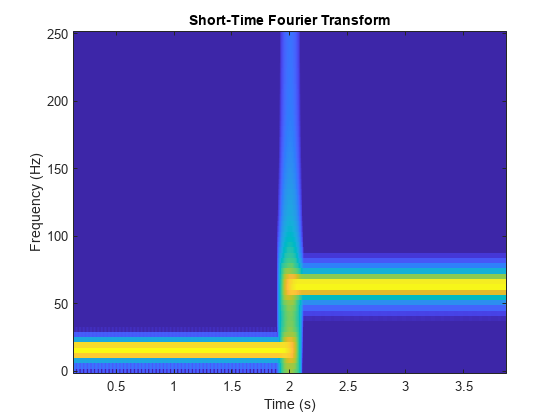
Linear Chirp
Generate a linear chirp sampled at 1 kHz.
Fs = 1e3; frq = 128; t = 0:1/Fs:2; sig = sin(2*pi*frq*t.^2);
Plot the magnitude of the wavelet packet power spectrum.
clf wpt = wpdec(sig,level,"sym8"); [Spec,Time,Freq] = wpspectrum(wpt,Fs,"plot");

Compare with a plot of the magnitude of the STFT.
stft(sig,Fs,Window=window,OverlapLength=noverlap, ... FrequencyRange="onesided") colorbar off colormap("default")

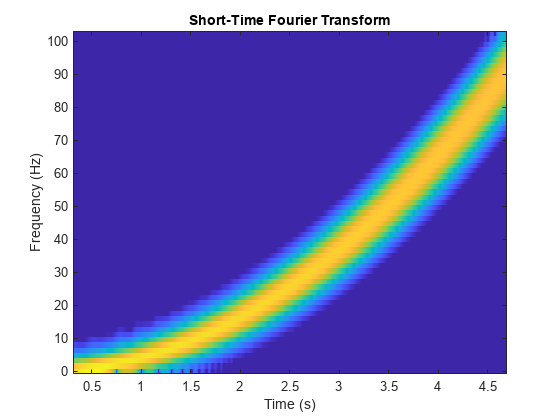
Quadratic Chirp
Generate a quadratic chirp.
sig = wnoise("quadchirp",10);
len = length(sig);
t = linspace(0,5,len);
Fs = 1/t(2);Plot the magnitude of the wavelet packet power spectrum.
clf wpt = wpdec(sig,level,"sym8"); [Spec,Time,Freq] = wpspectrum(wpt,Fs,"plot");

Compare with a plot of the magnitude of the STFT.
stft(sig,Fs,Window=window,OverlapLength=noverlap, ... FrequencyRange="onesided") colorbar off colormap("default")
Building Wavelet Packets
The computational scheme for wavelet packets generation is easy when using an orthogonal wavelet. We start with the two filters of length , and , that correspond to the wavelet.
Now by induction, let us define the sequence of functions by:
where is the scaling function and is the wavelet function.
For example, for the Haar wavelet we have
and
The equations become
and
is the Haar scaling function, and is the Haar wavelet. Both functions are supported in the closed interval [-1,1]. Then we can obtain by adding half-scaled versions of with distinct supports [0,1/2] and [1/2,1].
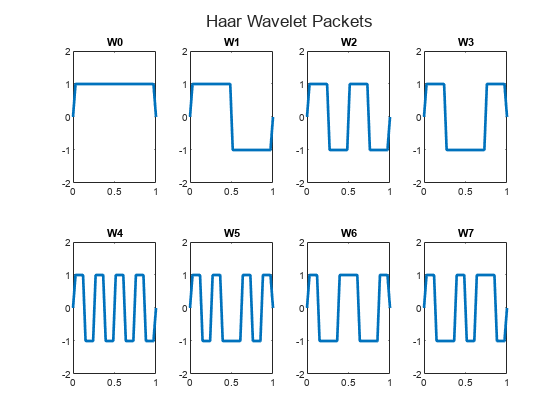
Use the wpfun function to plot the -functions associated with the Haar wavelet on a 1/2^5 grid.
[wfun,xgrid] = wpfun("db1",7,5); t = tiledlayout(2,4); for k=0:7 nexttile plot(xgrid,wfun(k+1,:),LineWidth=2) title("W"+num2str(k)) ylim([-2 2]) end title(t,"Haar Wavelet Packets")
Starting from more regular original wavelets and using a similar construction, we obtain smoothed versions of this system of W-functions, all with support in the interval [0, 2N–1].
Use the wpfun function to plot the -functions associated with the db2 wavelet.
[wfun,xgrid] = wpfun("db2",7,5); t = tiledlayout(2,4); for k=0:7 nexttile plot(xgrid,wfun(k+1,:),LineWidth=2) title("W"+num2str(k)) ylim([-3 3]) end title(t,"db2 Wavelet Packets")

Wavelet Packet Atoms
Starting from the functions and following the same line leading to orthogonal wavelets, we consider the three-indexed family of analyzing functions (the waveforms):
where and .
As in the wavelet framework, k can be interpreted as a time-localization parameter and j as a scale parameter. So what is the interpretation of n?
The basic idea of wavelet packets is that for fixed values of j and k, Wj,n,k analyzes the fluctuations of the signal roughly around the position 2j· k, at the scale 2j, and at various frequencies for the different admissible values of the last parameter n.
In fact, examining carefully the wavelet packets displayed in Haar
Wavelet Packets and db2
Wavelet Packets, the naturally ordered
Wn for n = 0, 1,
..., 7, does not match exactly the order defined by the number of oscillations. More
precisely, counting the number of zero crossings (up-crossings and down-crossings)
for the db1 wavelet packets, we have the following.
So, to restore the property that the main frequency increases monotonically with the order, it is convenient to define the frequency order obtained from the natural one recursively.
As can be seen in the previous figures, Wr(n)(x) “oscillates”
approximately n times.
To analyze a signal (the Linear Chirp, for instance), it is better to plot the wavelet packet coefficients following the frequency order from the low frequencies at the bottom to the high frequencies at the top, rather than naturally ordered coefficients.
To plot the coefficients in a wavelet packet tree, use the wpviewcf function.
Organizing the Wavelet Packets
The set of functions is the (j,n) wavelet packet. For positive values of integers j and n, wavelet packets are organized in trees. The tree in the figure Wavelet Packets Organized in a Tree; Scale j Defines Depth and Frequency n Defines Position in the Tree is created to give a maximum level decomposition equal to 3. For each scale j, the possible values of parameter n are 0, 1, ..., 2j–1.
Wavelet Packets Organized in a Tree; Scale j Defines Depth and Frequency n Defines Position in the Tree

The notation Wj,n, where j denotes the scale parameter and n the frequency parameter, is consistent with the usual depth-position tree labeling.
We have , and .
It turns out that the library of wavelet packet bases contains the wavelet basis and several other bases. Let us have a look at some of those bases. More precisely, let V0 denote the space (spanned by the family W0,0) in which the signal to be analyzed lies; then {Wd,1; d ≥ 1} is an orthogonal basis of V0.
For every strictly positive integer D, {WD,0, {Wd,1; 1 ≤ d ≤ D}} is an orthogonal basis of V0.
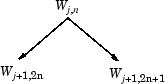
We also know that the family of functions {(Wj+1,2n), (Wj+1,2n+1)} is an orthogonal basis of the space spanned by Wj,n, which is split into two subspaces: Wj+1,2n spans the first subspace, and Wj+1,2n+1 the second one.
This last property gives a precise interpretation of splitting in the wavelet packet organization tree, because all the developed nodes are of the form shown in the figure Wavelet Packet Tree: Split and Merge.
It follows that the leaves of every connected binary subtree of the complete tree correspond to an orthogonal basis of the initial space.
For a finite energy signal belonging to V0, any wavelet packet basis will provide exact reconstruction and offer a specific way of coding the signal, using information allocation in frequency scale subbands.
Choosing Optimal Decomposition
Based on the organization of the wavelet packet library, it is natural to count the decompositions issued from a given orthogonal wavelet.
A signal of length can be expanded in different ways, where is the number of binary subtrees of a complete binary tree of depth L. As a result, (see [1]).
As this number may be very large, and since explicit enumeration is generally unmanageable, it is interesting to find an optimal decomposition with respect to a convenient criterion, computable by an efficient algorithm. We are looking for a minimum of the criterion.
Functions satisfying an additivity-type property are well suited for efficient searching of binary-tree structures and the fundamental splitting. Classical entropy-based criteria match these conditions and describe information-related properties for an accurate representation of a given signal. Entropy is a common concept in many fields, mainly in signal processing. Let us list four different entropy criteria (see [2]); many others are available and can be easily integrated (see wpdec). In the following expressions s is the signal and (si) are the coefficients of s in an orthonormal basis.
The entropy must be an additive cost function with that and .
The (nonnormalized) Shannon entropy, , so , with the convention .
The concentration in norm with , , so .
The logarithm of the "energy" entropy, , so , with the convention .
The threshold entropy, if , and otherwise, so such that is the number of time instants when the signal is greater than a threshold .
Compute Various Entropies
Generate a signal of energy equal to 1.
s = ones(1,16)*0.25;
Compute the Shannon entropy of s.
e1 = -sum((s.^2).*log(s.^2))
e1 = 2.7726
Compute the entropy of s.
e2 = norm(s,1.5)^1.5
e2 = 2.0000
Compute the "log energy" entropy of s.
e3 = sum(log(s.^2))
e3 = -44.3614
Compute the threshold entropy of s, using a threshold value of 0.24.
e4 = sum(abs(s)>0.24)
e4 = 16
Minimum-Entropy Decomposition
This simple example illustrates the use of entropy to determine whether a new splitting is of interest to obtain a minimum-entropy decomposition.
For convenience, first define an anonymous function that computes the Shannon entropy for signals with strictly nonzero values.
shannon = @(x)(-sum((x.^2).*log(x.^2)));
Construct a constant signal.
w00 = ones(1,16)*0.25;
Compute the Shannon entropy of the signal.
e00 = shannon(w00)
e00 = 2.7726
Use the dwt function to split w00 using the Haar wavelet.
[w10,w11] = dwt(w00,"db1");Compute the entropy of the approximation at level 1.
e10 = shannon(w10)
e10 = 2.0794
Because the original signal is constant, the detail at level 1 is 0. Therefore, the entropy is 0. Due to the additivity property, the entropy of the decomposition is given by e10 + e11 = 2.0794. Compare the sum to the initial entropy e00 = 2.7726. We have e10 + e11 < e00, so splitting reduces the entropy.
Split the approximation w10.
[w20,w21] = dwt(w10,"db1");We have w20=0.5*ones(1,4) and w21 is zero. Compute the entropy of the approximation at level 2.
e20 = shannon(w20)
e20 = 1.3863
We have e20 + 0 < e10, so again, splitting makes the entropy decrease.
Iterate the splitting two more times.
[w30,w31] = dwt(w20,"db1");
e30 = shannon(w30)e30 = 0.6931
[w40,w41] = dwt(w30,"db1")w40 = 1.0000
w41 = 0
e40 = shannon(w40)
e40 = -4.4409e-16
In the last splitting operation, we find that only one piece of information is needed to reconstruct the original signal. The wavelet basis at level 4 is a best basis with respect to Shannon entropy. Because e40 + e41 + e31 + e21 + e11 = 0, the basis has minimum entropy.
Use the wpdec function to compute the wavelet packet decomposition of the original signal.
t = wpdec(w00,4,"haar","shannon");
The wavelet packet tree t is a binary tree with four levels. Plot a binary tree with the nodes labeled with the original entropy values. Use the helper function helperPlotTreeWithLabels. Source code for the helper function is in the same directory as this example file.
helperPlotTreeWithLabels([e00,e10,e20,e30])
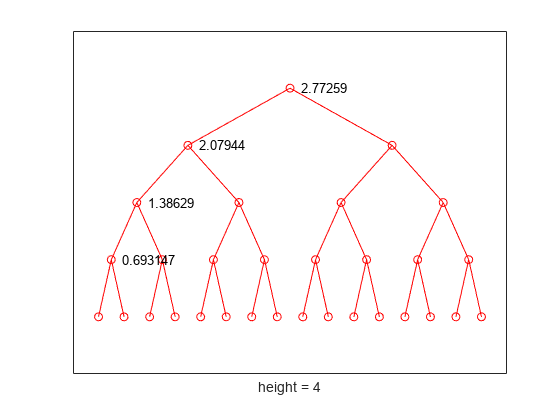
Compute the best tree. Plot the best tree. In this case, the best tree corresponds to the wavelet tree.
bt = besttree(t); plot(bt)

Some Interesting Subtrees
Using wavelet packets requires tree-related actions and labeling. The implementation of the user interface is built around this consideration. For more information on the technical details, see the reference pages.
The complete binary tree of depth D corresponding to a wavelet packet decomposition tree developed at level D is denoted by WPT.
We have the following interesting subtrees.
Decomposition Tree | Subtree Such That the Set of Leaves Is a Basis |
|---|---|
Wavelet packets decomposition tree | Complete binary tree: WPT of depth D |
Wavelet packets optimal decomposition tree | Binary subtree of WPT |
Wavelet packets best-level tree | Complete binary subtree of WPT |
Wavelet decomposition tree | Left unilateral binary subtree of WPT of depth D |
Wavelet best-basis tree | Left unilateral binary subtree of WPT |
We deduce the following definitions of optimal decompositions, with respect to an entropy criterion E.
Decompositions | Optimal Decomposition | |
|---|---|---|
Wavelet packet decompositions | Search among 2D trees | Search among D trees |
Wavelet decompositions | Search among D trees | Search among D trees |
For any nonterminal node, we use the following basic step to find the optimal subtree with respect to a given entropy criterion E (where Eopt denotes the optimal entropy value).
Entropy Condition | Action on Tree and on Entropy Labeling |
|---|---|
| If (node≠root), merge and set Eopt(node) = E(node) |
Split and set |
with the natural initial condition on the reference tree, Eopt(t) = E(t) for
each terminal node t.
Reconstructing Signal Approximation From a Node
You can use the wprcoef function to reconstruct an approximation to your signal from any node in the wavelet packet tree. This is true irrespective of whether you are working with a full wavelet packet tree, or a subtree determined by an optimality criterion. To extract the wavelet packet coefficients from a node without reconstructing an approximation to the signal, use the wpcoef function.
Load the noisy Doppler signal. Save the current extension mode.
load noisdopp origMode = dwtmode("status","nodisp");
Compute the wavelet packet decomposition down to level 5 using the sym4 wavelet. Use the periodization mode. Plot the tree.
dwtmode("per","nodisp") T = wpdec(noisdopp,5,"sym4"); plot(T)

Click on the (4,1) doublet (node 16) to get the following figure.
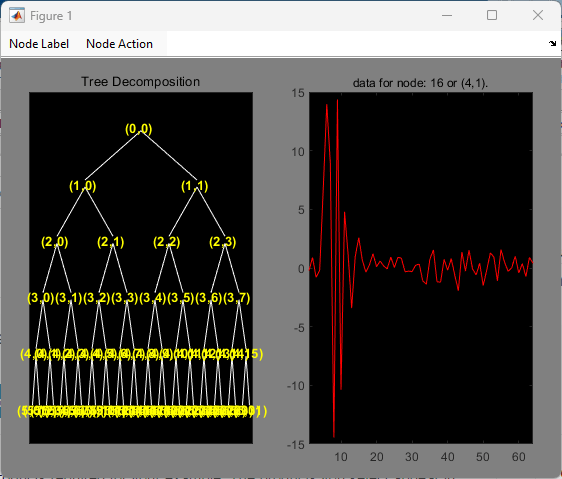
Use the wpcoef function to extract the wavelet packet coefficients from node 16. Obtain the length of the coefficients.
wpc = wpcoef(T,16); length(wpc)
ans = 64
Use the wprcoef function to obtain an approximation to the signal from node 16. Confirm the length of the approximation is equal to the length of the original signal.
rwpc = wprcoef(T,16); isequal(length(rwpc),length(noisdopp))
ans = logical
1
Compare the approximation with the original signal.
plot(noisdopp,"k") hold on plot(rwpc,"b",LineWidth=2) axis tight legend("Original","Approximation") hold off

Determine the optimum binary wavelet packet tree. Plot the tree.
Topt = besttree(T); plot(Topt)
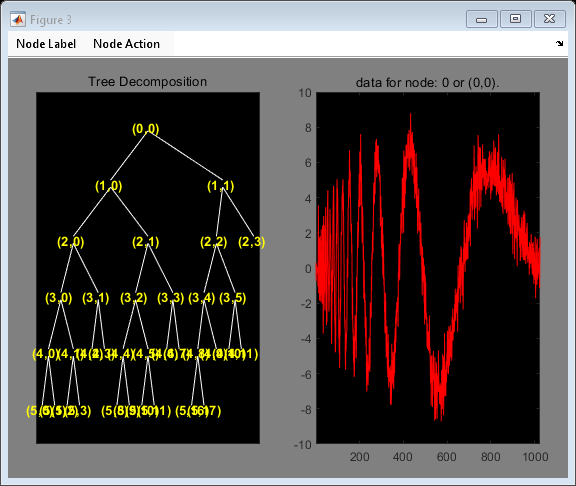
Click on the (3,0) doublet (node 17) to get the following figure.

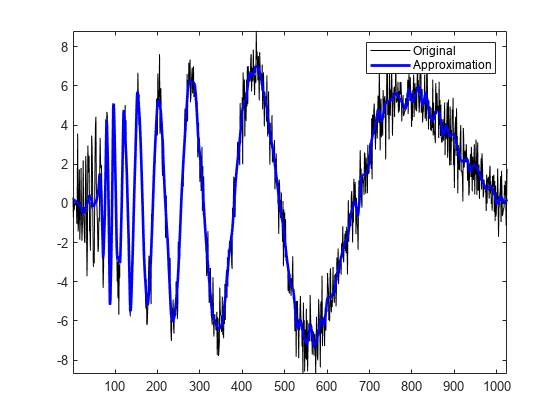
Reconstruct an approximation to the signal from the (3,0) doublet (node 7).
rsig = wprcoef(Topt,7); plot(noisdopp,"k") hold on plot(rsig,"b",LineWidth=2) axis tight legend("Original","Approximation") hold off
If you know which doublet in the binary wavelet packet tree you want to extract, you can determine the node corresponding to that doublet with the depo2ind function. Determine the node corresponding to the doublet (3,0).
Node = depo2ind(2,[3 0])
Node = 7
Restore the original extension mode.
dwtmode(origMode,"nodisp")Wavelet Packets 2-D Decomposition Structure
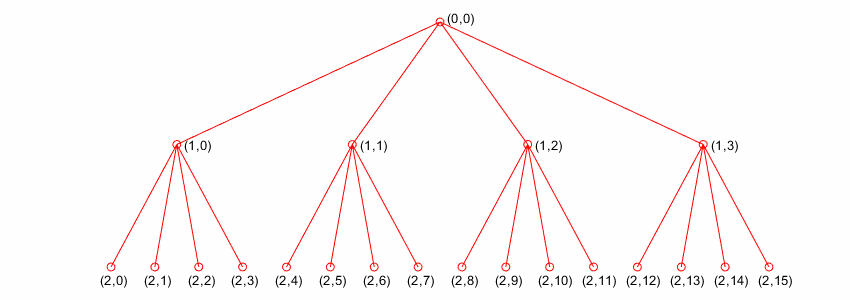
Exactly as in the wavelet decomposition case, the preceding 1-D framework can be extended to image analysis. Minor direct modifications lead to quaternary tree-related definitions. An example is shown the following figure for depth 2.
Wavelet Packets for Compression and Denoising
In the wavelet packet framework, compression and denoising ideas are identical to those
developed in the wavelet framework. The only new feature is a more complete analysis
that provides increased flexibility. A single decomposition using wavelet packets
generates a large number of bases. You can then look for the best representation
with respect to a design objective, using the
besttree function with an entropy
function.
References
[1] Mallat, S. G., and Gabriel Peyré. A Wavelet Tour of Signal Processing: The Sparse Way. 3rd ed. Amsterdam: Elsevier/Academic Press, 2009.
[2] Coifman, R.R., and M.V. Wickerhauser. “Entropy-Based Algorithms for Best Basis Selection.” IEEE Transactions on Information Theory 38, no. 2 (March 1992): 713–18. https://doi.org/10.1109/18.119732.