Optimize FPGA and ASIC Speed and Area Using HDL Coder
Overview
Learn how to use HDL Coder optimization and design techniques to meet your target-specific speed and area goals. HDL Coder offers techniques that span from automatic to fully-controlled, and all of them allow for rapid exploration of implementation options. This webinar will explain these options and their associated benefits and tradeoffs, including verification considerations, and will discuss techniques specific to FPGA and ASIC designs. All of these techniques will be demonstrated using the pulse detection design from the HDL Self-Guided Tutorial.
Highlights
- Workflow options from rapid estimation to running full synthesis and implementation
- Optimizing for speed
- Latency vs throughput vs clock frequency
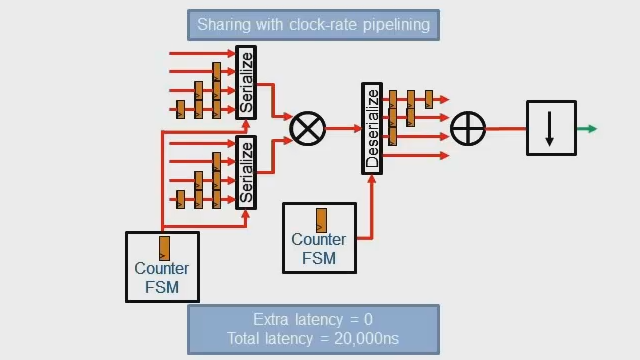
- Pipelining techniques
- Vector processing
- Multiplier mapping
- Optimizing for area
- Resource sharing
- RAM mapping
- Loop streaming of vector operations
About the Presenter
Eric Cigan is a principal product marketing manager at MathWorks for ASIC and FPGA verification. Prior to joining MathWorks, he held technical marketing roles at Mentor Graphics, MathStar, and AccelChip. Eric earned BS and MS degrees in mechanical engineering from the Massachusetts Institute of Technology. In his spare time, Eric curates a wide-ranging, ever-growing collection of FPGA development boards from manufacturers around the world.
Recorded: 28 Jul 2022