Performing Hardware and Software Co-design for Xilinx RFSoCs Gen3 Devices using MATLAB and Simulink
Overview
Learn how to use Model-Based Design to evaluate algorithm performance on hardware/software platforms like Xilinx UltraScale+ RFSoC Gen 3 devices. In this webinar, a MathWorks engineer demonstrates how Simulink and SoC Blockset are used to model range-Doppler radar algorithm implemented on Xilinx RFSoC devices. The presenter demonstrates how to make design decisions using SoC Blockset with C and HDL code generation by evaluating different hardware/software partitioning strategies.
Highlights
- Overview of Xilinx UltraScale+ RFSoC Gen 3 devices and their applications in wireless communications, aerospace/defense and test & measurement
- Introduction to the range-Doppler radar application and the specifications for the design
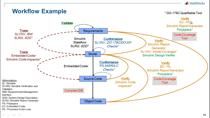
- Simulation of a high-level behavioral system model that serves as a golden reference for the hardware-software implementation on the RFSoC device and an elaborated implementation model for code generation
- Analysis of two alternative ways to perform hardware/software partitioning of the range-Doppler algorithm, using simulation and on-device profiling to determine the latency and implementation complexity
About the Presenter
Tom Mealey is a Senior Application Engineer at MathWorks. He supports customers in adopting Model-Based Design to accelerate the design and deployment of complex control and algorithmic applications including communications, radar, computer vision, audio, and deep learning. He is an expert on the design and implementation of applications targeting the Xilinx Zynq platform and other SoC devices. Prior to working at MathWorks, Tom worked at the Air Force Research Laboratory’s Sensors Directorate, where he was involved in projects implementing digital signal processing on FPGAs and SoCs. Tom earned his B.S. in Computer Engineering from the University of Notre Dame and his M.S. in Electrical Engineering from the University of Dayton.
Recorded: 29 Jul 2021