rpmak
Put together rational spline
Syntax
rp = rpmak(breaks,coefs)
rp = rpmak(breaks,coefs,d)
rpmak(breaks,coefs,sizec)
rs = rsmak(knots,coefs)
rs
= rsmak(shape,parameters)
Description
Both rpmak and rsmak put together a rational spline from minimal information. rsmak is
also equipped to provide rational splines that describe standard geometric shapes. A
rational spline must be scalar- or vector-valued.
rp = rpmak(breaks,coefs) has the same
effect as the command ppmak(breaks, coefs) except that the
resulting ppform is tagged as a rational spline, i.e., as a rpform.
To describe what this means, let R be the piecewise-polynomial
put together by the command ppmak(breaks,coefs), and let
r(x) =
s(x)/w(x)
be the rational spline put together by the command
rpmak(breaks,coefs). If v is the value of
R at x, then
v(1:end-1)/v(end) is the value of r at
x. In other words, R(x)
=
[s(x);w(x)].
Correspondingly, the dimension of the target of r is one less
than the dimension of the target of R. In particular, the
dimension (of the target) of R must be at least 2, i.e., the
coefficients specified by coefs must be
d-vectors with d > 1. See
ppmak for how the input arrays
breaks and coefs are being interpreted,
hence how they are to be specified in order to produce a particular
piecewise-polynomial.
rp = rpmak(breaks,coefs,d) has the same
effect as ppmak(breaks,coefs,d+1), except that the resulting
ppform is tagged as being a rpform. Note that the desire to have that optional third
argument specify the dimension of the target requires different values for it in
rpmak and ppmak for the same coefficient
array coefs.
rpmak(breaks,coefs,sizec) has the same
effect as ppmak(breaks,coefs,sizec) except that the resulting
ppform is tagged as being a rpform, and the target dimension is taken to be
sizec(1)-1.
rs = rsmak(knots,coefs) is similarly
related to spmak(knots,coefs), and
rsmak(knots,coefs,sizec) to
spmak(knots,coefs,sizec). In particular,
rsmak(knots,coefs) puts together a rational spline in B-form,
i.e., it provides a rBform. See spmak for how the input arrays
knots and coefs are being interpreted,
hence how they are to be specified in order to produce a particular
piecewise-polynomial.
rs
= rsmak(shape,parameters) provides a rational spline in rBform that
describes the shape being specified by the character vector or string scalar
shape and the optional additional
parameters. Specific choices are:
rsmak('arc',radius,center,[alpha,beta])
rsmak('circle',radius,center)
rsmak('cone',radius,halfheight)
rsmak('cylinder',radius,height)
rsmak('southcap',radius,center)
rsmak('torus',radius,ratio)
with 1 the default value for radius,
halfheight and height, and the origin the
default for center, and the arc running through all the angles
from alpha to beta (default is
[-pi/2,pi/2]), and the cone, cylinder, and torus centered at
the origin with their major circle in the (x,y)-plane, and the minor circle of the
torus having radius radius*ratio, the default for
ratio being 1/3.
From these, one may generate related shapes by affine transformations, with the
help of fncmb(rs,transformation).
All fn... commands except fnint,
fnder, fndir can handle rational
splines.
Examples
The commands
runges = rsmak([-5 -5 -5 5 5 5],[1 1 1; 26 -24 26]); rungep = rpmak([-5 5],[0 0 1; 1 -10 26],1);
both provide a description of the rational polynomial
r(x) =
1/(x2 + 1) on the interval [-5 ..
5]. However, outside the interval [-5 .. 5], the function given by
runges is zero, while the rational spline given by
rungep agrees with
1/(x2 + 1) for every
x.
The figure of a rotated cone is generated by the commands
fnplt(fncmb(rsmak('cone',1,2),[0 0 -1;0 1 0;1 0 0]))
axis equal, axis off, shading interp
A Rotated Cone Given by a Rational Quadratic Spline

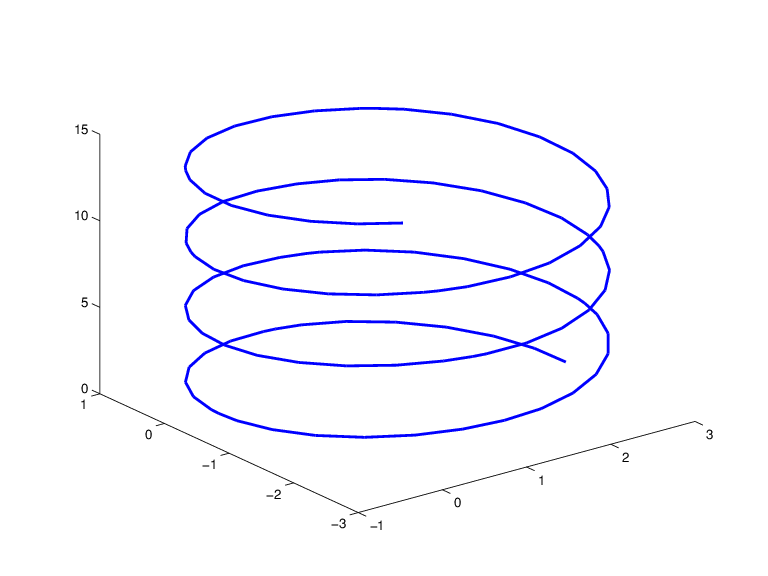
A Helix, showing a helix with several windings, is generated by the commands
arc = rsmak('arc',2,[1;-1],[0 7.3*pi]);
[knots,c] = fnbrk(arc,'k','c');
helix = rsmak(knots, [c(1:2,:);aveknt(knots,3).*c(3,:);
c(3,:)]);
fnplt(helix)
A Helix
For further illustrated examples, see NURBS and Other Rational Splines