Counterbalance Valve
(To be removed) Hydraulic counterbalance valve
The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead.
For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.
Libraries:
Simscape /
Fluids /
Hydraulics (Isothermal) /
Valves /
Flow Control Valves
Description
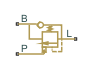
Counterbalance valves are used in hydraulic systems working with an overriding (run-away) or suspended load. They are designed to create backpressure at the return line of the actuator to prevent losing control over the load. The following illustration shows a counterbalance valve schematic.

If a directional valve (not shown in the picture) is shifted into position that lowers the load, then the fluid from the rod chamber of the cylinder can exit only if pressure at port P (pilot pressure) and port L (load pressure) create enough force to overcome the spring force and open the valve. In statics, the valve is described with the equation
| (1) |
where
| F0 | Spring setting |
| c | Spring rate |
| x | Valve opening |
| ppilot | Pilot pressure (pressure at port P) |
| pload | Load pressure (pressure at port L) |
| pback | Backpressure (pressure at return port B) |
| Apilot | Valve effective area at pilot port P |
| Aload | Valve effective area at load port L |
| Aback | Valve effective area at return port B |
Counterbalance valve, classified by type, is an internally-externally piloted valve because both the pilot pressure and the load pressure tend to open the valve. After minor rearrangements, Equation 1 takes the form
| (2) |
where
| pset | Valve pressure setting |
| cp | Spring pressure stiffness (Pa/m) |
| x | Valve opening |
| kpilot | Pilot ratio |
| kback | Backpressure ratio |
The valve displacement is determined from Equation 2:
| (3) |
where xmax is the maximum valve displacement.
The Counterbalance Valve block can be represented as the following structural model.

The pressure sensors measure pressure at respective ports and convey their values to the Fcn block, which, together with the PS Saturation block, performs calculations in accordance with Equation 3. The valve displacement is passed through the first order lag block, built of the PS Subtract, PS Gain, and PS Integrator blocks, to account for valve dynamics. The gain of the PS Gain block is set to 1/T, where T is the time constant. The Variable Orifice and Check Valve blocks simulate the counterbalance valve orifice and check valve. In the actual Counterbalance Valve block model, the operations performed by the sensors and the Fcn block are executed in the block equation section.
The Counterbalance Valve block is essentially a data-sheet-based model. Depending on data listed in the manufacturer's catalogs or data sheets for your particular valve, you can choose one of the following model parameterization options:
By maximum area and opening— Use this option if the data sheet provides only the orifice maximum area and the control member maximum stroke.By area vs. opening table— Use this option if the catalog or data sheet provides a table of the orifice passage area based on the control member displacement.
In the latter case, the PS Saturation block in the structural model is replaced with the PS Lookup Table (1D) block, and you can choose from three interpolation and two extrapolation methods.
Connections L and B are hydraulic conserving ports associated with the load and backpressure ports of the valve. The hydraulic conserving port P is associated with the pilot port. The block positive direction is from port L to port B. Positive pressure at port P opens the valve.
Assumptions and Limitations
Valve dynamics are approximated by introducing the first order lag between the pressure sensors and the variable orifice control member displacement.
Inertia, friction, or hydraulic forces acting on the valve control member are not taken into account.