andrewsplot

Andrews plot

Syntax

andrewsplot(X)

andrewsplot(X,Name=Value)

andrewsplot(ax,___)

p = andrewsplot(___)

Description

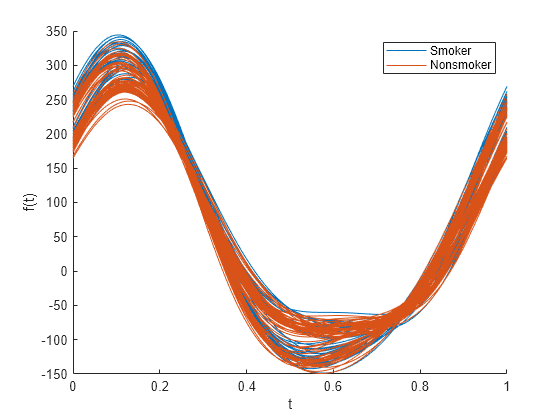
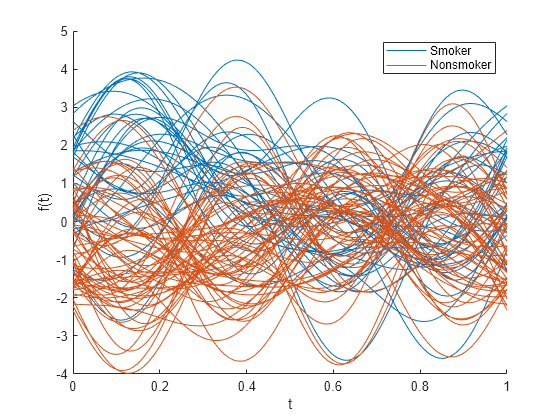
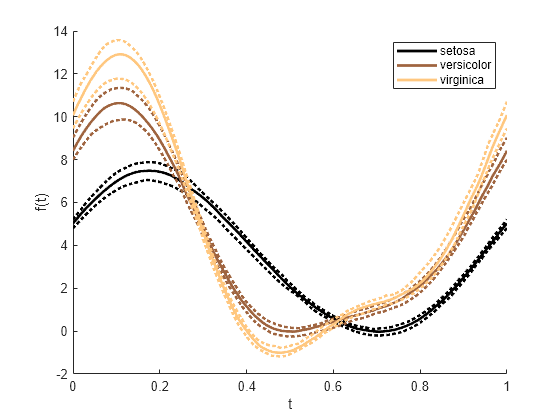
andrewsplot(X) creates an Andrews plot of the multivariate data in the matrix X. The plot displays a continuous curve for each observation in X. For more information, see Andrews Plot.

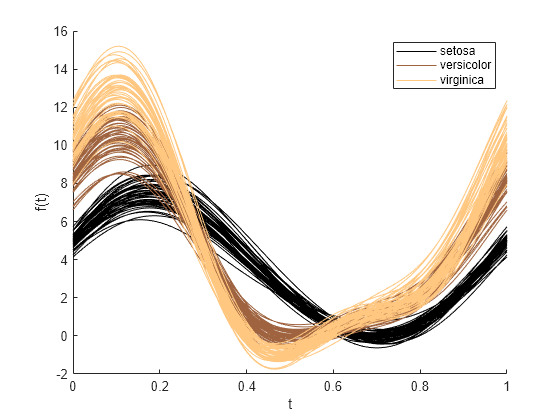
andrewsplot(X,Name=Value) specifies additional options using one or more name-value arguments. For example, you can standardize the data in X before plotting, and group the data using a grouping variable.

andrewsplot(ax,___) displays the plot in the target axes ax. Specify the axes as the first input argument in any of the previous syntaxes.

p = andrewsplot(___) returns an array of Line objects using any of the input argument combinations in the previous syntaxes. Use p to modify properties of the plot after creating it. For a list of properties, see Line Properties.

Examples

Visualize Grouped Data

Create an Andrews plot to visualize grouped sample data.

Load the fisheriris data set, which contains four measurements (sepal length, sepal width, petal length, and petal width) from three species of iris flowers.

load fisheriris

The matrix meas contains all four measurements for 150 flowers. The cell array species contains the species name for each of the 150 flowers.

Create an Andrews plot, grouping the sample data by species.

andrewsplot(meas,Group=species)

The plot displays each observation (flower) as a smooth function over the interval [0,1]. The color of each curve indicates the flower species.

Create a second, simplified Andrews plot that displays only the median and quartiles of each group.

andrewsplot(meas,Group=species,Quantile=0.25)

The plot shows the median values for each group as a solid curve and the values for the other quartiles as dotted curves of the same color.

Differentiate Between Groups Using Standardization and Quartiles

Visualize multidimensional data by using Andrews plots. First, group the data. Then, use standardization and quartiles to see the difference between the groups.

Load the patients data set, which contains medical information for 100 patients. Specify the descriptive category names Smoker and Nonsmoker rather than 1 and 0. Then, create a table using the Diastolic, Systolic, Weight, Age, and Smoker variables.

load patients
Smoker = categorical(Smoker,logical([1 0]), ...
    ["Smoker","Nonsmoker"]);
patientData = table(Diastolic,Systolic,Weight,Age,Smoker);

Create an Andrews plot from the variables in patientData. Use the last variable to group the data by smoker status.

andrewsplot(patientData{:,1:end-1},Group=patientData.Smoker)

By default, the plot uses unstandardized data. The plot does not show a great difference between Smoker and Nonsmoker groups.

Standardize the numeric patientData variables before plotting.

andrewsplot(patientData{:,1:end-1},Group=Smoker,Standardize="on")

The resulting Andrews plot shows more variation between the Smoker and Nonsmoker groups. The plot is slightly crowded because it shows 100 curves, one for each patient in patientData.

Instead of displaying a curve for each observation, show the quartile curves for each group. The quartiles consist of the 25th percentile, median, and 75th percentile.

andrewsplot(patientData{:,1:end-1},Group=patientData.Smoker, ...
    Standardize="on",Quantile=0.25)

The quartile curves show differences between the Smoker and Nonsmoker groups. For example, at approximately 0.25, the two groups have quartile values that do not overlap.

Recall that each function displayed in the Andrews plot is a linear combination of the variables, whose coefficients change over time. (See Andrews Plot.) Compute the coefficients for the variables at time 0.25. This linear combination of the variables can help you differentiate between the groups.

t = 0.25;
variables = patientData.Properties.VariableNames(1:end-1)

variables = 1×4 cell
    {'Diastolic'}    {'Systolic'}    {'Weight'}    {'Age'}

coefficients = [1/sqrt(2) sin(2*pi*t) cos(2*pi*t) sin(4*pi*t)]

coefficients = 1×4

    0.7071    1.0000    0.0000    0.0000

At time 0.25, the Diastolic and Systolic variables have positive coefficients of similar magnitude, and the Weight and Age variables have 0 coefficients. The previous plot shows that, after the standardization of the data, the quartile curves for the Smoker group have positive values at time 0.25, and the quartile curves for the Nonsmoker group have negative values at time 0.25.

The plot and variable coefficients indicate that patients in the Smoker group tend to have higher Diastolic and Systolic values, providing one way to distinguish between the Smoker and Nonsmoker groups in patientData.

Adjust Plot Appearance

Adjust the appearance of an Andrews plot. You can set some plot properties in the call to andrewsplot. You can also specify the appearance of the plot before or after creating it.

Load the fisheriris data set, which contains four measurements (sepal length, sepal width, petal length, and petal width) from three species of iris flowers.

load fisheriris

The matrix meas contains all four measurements for 150 flowers. The cell array species contains the species name for each of the 150 flowers.

Create an Andrews plot using the measurement data in meas and the group data in species. Specify a nondefault color scheme (copper) for the grouped data by setting the color order before plotting.

colororder(copper(3))
andrewsplot(meas,Group=species)

Plot only the median, 25th percentile, and 75th percentile curves for each group in species. To make the plot lines thicker, specify the line width as 2. When you specify the LineWidth value in the call to andrewsplot, the function sets the line width of every curve in the plot to the same value.

andrewsplot(meas,Group=species,Quantile=0.25,LineWidth=2)

Recreate the previous plot, but increase the line width of only the curve representing the median measurements for the irises in the setosa group. First, create an array of Line objects p, where each object corresponds to a curve in the plot. Then, modify the LineWidth property of the first Line object in the array by using dot notation.

p = andrewsplot(meas,Group=species,Quantile=0.25)

p = 
  9×1 Line array:

  Line    (median)
  Line    (lower quantile)
  Line    (upper quantile)
  Line    (median)
  Line    (lower quantile)
  Line    (upper quantile)
  Line    (median)
  Line    (lower quantile)
  Line    (upper quantile)

p(1).LineWidth = 2;

Input Arguments

X — Multivariate data

numeric matrix

Multivariate data, specified as a numeric matrix. The rows of X correspond to observations, and the columns correspond to variables.

andrewsplot treats NaN values in X as missing values and ignores the corresponding rows.

Example: rand(100,10)

Data Types: single | double

ax — Axes for plot

Axes object

Axes for the plot, specified as an Axes object. If you do not specify ax, then andrewsplot creates the plot using the current axes. For more information on creating an Axes object, see axes.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: andrewsplot(meas,Group=species,Quantile=0.25) specifies to plot the median, 25th percentile, and 75th percentile curves for each group in species.

Group — Variable for grouping data

numeric vector | logical vector | character matrix | string array | cell array of character vectors | categorical vector

Variable for grouping data, specified as a numeric vector, logical vector, character matrix, string array, cell array of character vectors, or categorical vector. Specify a group value for each observation in X.

The andrewsplot function uses color to differentiate between groups. That is, observations in the same group have curves of the same color. By default, andrewsplot assigns a maximum of seven unique group colors. When the total number of groups exceeds the number of colors, the function cycles through the colors. For an example on how to adjust the colors in an Andrews plot for a specific number of groups, see Adjust Plot Appearance.

Example: Group=["good","bad","bad","good","good","bad","bad","bad"]

Data Types: single | double | logical | char | string | cell | categorical

Quantile — Quantiles of data to plot

numeric scalar in the range (0,1)

Quantiles of the data to plot, specified as a numeric scalar in the range (0,1). When you specify Quantile as a value α, the andrewsplot function plots only the median, α, and 1 – α quantiles of f(t) at each value of t.

The quantile plot option provides a useful summary of the data when X contains many observations.

Example: Quantile=0.25

Data Types: single | double

Standardize — Method for standardizing data

"off" (default) | "on" | "pca" | "pcastd"

Method for standardizing the data, specified as one of the values in this table.

Value	Description
"off"	Use unstandardized X data.
"on"	Scale each column of X to have a mean equal to 0 and a standard deviation equal to 1 before plotting.
"pca"	Create a plot from the principal component scores of X, in order of decreasing eigenvalues.
"pcastd"	Create a plot using the standardized principal component scores.

For more information on principal component analysis, see pca.

Example: Standardize="pca"

Data Types: char | string

Output Arguments

p — Objects for plot modification

array of Line objects

Objects to use for plot modification, returned as an array of Line objects.

• If you do not specify a quantile value (Quantile), then p contains one object for each row of X.

• If you specify a quantile value, then p contains three objects for each group in the grouping variable (Group).

More About

Andrews Plot

An Andrews plot displays observations by using functions f(t) of a continuous dummy variable t over the interval [0,1]. For observation i in X, the function f_i(t) is defined as:

$$f_i(t)=\frac{X(i,1)}{\sqrt{2}}+X(i,2)\cdot \sin (2\pi t)+X(i,3)\cdot \cos (2\pi t)+X(i,4)\cdot \sin (4\pi t)+\dots$$

Tips

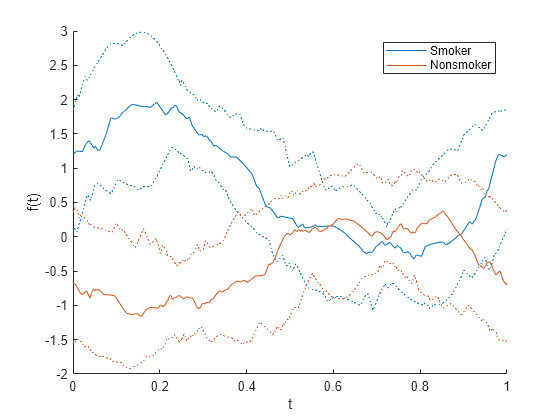
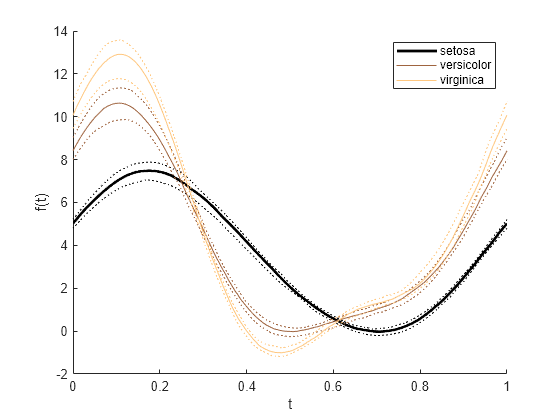
• You can modify certain aspects of the plot curves by specifying a property name and value for any of the properties listed in Line Properties. However, this approach applies the modification to all the curves in the plot. To modify only certain plot curves, use the syntax that returns Line objects and use dot notation to adjust each object property individually. For an example, see Adjust Plot Appearance.

Version History

Introduced before R2006a