fit
Description
The fit function fits a configured naive Bayes classification model for incremental learning (incrementalClassificationNaiveBayes object) to streaming data. To additionally track performance metrics using the data as it arrives, use updateMetricsAndFit instead.
To fit or cross-validate a naive Bayes classification model to an entire batch of data at once, see fitcnb.
Mdl = fit(Mdl,X,Y)Mdl, which represents the input naive Bayes classification model for
incremental learning Mdl trained using the predictor and response
data, X and Y respectively. Specifically,
fit updates the conditional posterior distribution of the
predictor variables given the data.
Examples
Fit an incremental naive Bayes learner when you know only the expected maximum number of classes in the data.
Create an incremental naive Bayes model. Specify that the maximum number of expected classes is 5.
Mdl = incrementalClassificationNaiveBayes('MaxNumClasses',5)Mdl =
incrementalClassificationNaiveBayes
IsWarm: 0
Metrics: [1×2 table]
ClassNames: [1×0 double]
ScoreTransform: 'none'
DistributionNames: 'normal'
DistributionParameters: {}
Properties, Methods
Mdl is an incrementalClassificationNaiveBayes model. All its properties are read-only. Mdl can process at most 5 unique classes. By default, the prior class distribution Mdl.Prior is empirical, which means the software updates the prior distribution as it encounters labels.
Mdl must be fit to data before you can use it to perform any other operations.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Fit the incremental model to the training data, in chunks of 50 observations at a time, by using the fit function. At each iteration:
Simulate a data stream by processing 50 observations.
Overwrite the previous incremental model with a new one fitted to the incoming observations.
Store the mean of the first predictor in the first class and the prior probability that the subject is moving (
Y> 2) to see how these parameters evolve during incremental learning.
% Preallocation numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); mu11 = zeros(nchunk,1); priormoved = zeros(nchunk,1); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = fit(Mdl,X(idx,:),Y(idx)); mu11(j) = Mdl.DistributionParameters{1,1}(1); priormoved(j) = sum(Mdl.Prior(Mdl.ClassNames > 2)); end
Mdl is an incrementalClassificationNaiveBayes model object trained on all the data in the stream.
To see how the parameters evolve during incremental learning, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(mu11) ylabel('\mu_{11}') xlabel('Iteration') axis tight nexttile plot(priormoved) ylabel('\pi(Subject Is Moving)') xlabel(t,'Iteration') axis tight
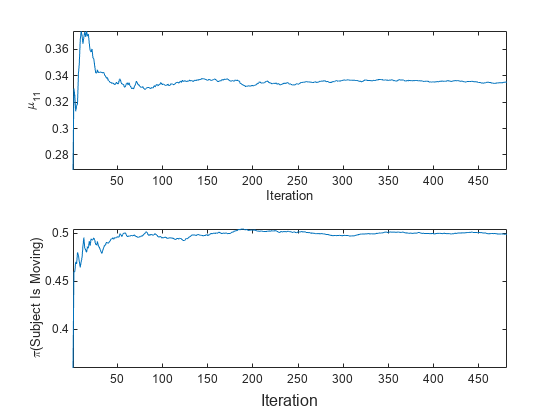
fit updates the posterior mean of the predictor distribution as it processes each chunk. Because the prior class distribution is empirical, (subject is moving) changes as fit processes each chunk.
Fit an incremental naive Bayes learner when you know all the class names in the data.
Consider training a device to predict whether a subject is sitting, standing, walking, running, or dancing based on biometric data measured on the subject. The class names map 1 through 5 to an activity. Also, suppose that the researchers plan to expose the device to each class uniformly.
Create an incremental naive Bayes model for multiclass learning. Specify the class names and the uniform prior class distribution.
classnames = 1:5; Mdl = incrementalClassificationNaiveBayes('ClassNames',classnames,'Prior','uniform')
Mdl =
incrementalClassificationNaiveBayes
IsWarm: 0
Metrics: [1×2 table]
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
DistributionNames: 'normal'
DistributionParameters: {5×0 cell}
Properties, Methods
Mdl is an incrementalClassificationNaiveBayes model object. All its properties are read-only. During training, observed labels must be in Mdl.ClassNames.
Mdl must be fit to data before you can use it to perform any other operations.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1); % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Fit the incremental model to the training data by using the fit function. Simulate a data stream by processing chunks of 50 observations at a time. At each iteration:
Process 50 observations.
Overwrite the previous incremental model with a new one fitted to the incoming observations.
Store the mean of the first predictor in the first class and the prior probability that the subject is moving (
Y> 2) to see how these parameters evolve during incremental learning.
% Preallocation numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); mu11 = zeros(nchunk,1); priormoved = zeros(nchunk,1); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = fit(Mdl,X(idx,:),Y(idx)); mu11(j) = Mdl.DistributionParameters{1,1}(1); priormoved(j) = sum(Mdl.Prior(Mdl.ClassNames > 2)); end
Mdl is an incrementalClassificationNaiveBayes model object trained on all the data in the stream.
To see how the parameters evolve during incremental learning, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(mu11) ylabel('\mu_{11}') xlabel('Iteration') axis tight nexttile plot(priormoved) ylabel('\pi(Subject Is Moving)') xlabel(t,'Iteration') axis tight
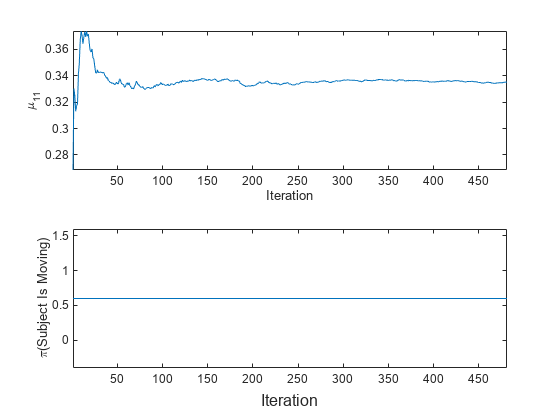
fit updates the posterior mean of the predictor distribution as it processes each chunk. Because the prior class distribution is specified as uniform, (subject is moving) = 0.6 and does not change as fit processes each chunk.
Train a naive Bayes classification model by using fitcnb, convert it to an incremental learner, track its performance on streaming data, and then fit the model to the data. Specify observation weights.
Load and Preprocess Data
Load the human activity data set. Randomly shuffle the data.
load humanactivity rng(1); % For reproducibility n = numel(actid); idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Suppose that the data from a stationary subject (Y <= 2) has double the quality of the data from a moving subject. Create a weight variable that assigns a weight of 2 to observations from a stationary subject and 1 to a moving subject.
W = ones(n,1) + (Y <=2);
Train Naive Bayes Classification Model
Fit a naive Bayes classification model to a random sample of half the data.
idxtt = randsample([true false],n,true);
TTMdl = fitcnb(X(idxtt,:),Y(idxtt),'Weights',W(idxtt))TTMdl =
ClassificationNaiveBayes
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
NumObservations: 12053
DistributionNames: {1×60 cell}
DistributionParameters: {5×60 cell}
Properties, Methods
TTMdl is a ClassificationNaiveBayes model object representing a traditionally trained naive Bayes classification model.
Convert Trained Model
Convert the traditionally trained model to a naive Bayes classification model for incremental learning.
IncrementalMdl = incrementalLearner(TTMdl)
IncrementalMdl =
incrementalClassificationNaiveBayes
IsWarm: 1
Metrics: [1×2 table]
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
DistributionNames: {1×60 cell}
DistributionParameters: {5×60 cell}
Properties, Methods
IncrementalMdl is an incrementalClassificationNaiveBayes model. Because class names are specified in IncrementalMdl.ClassNames, labels encountered during incremental learning must be in IncrementalMdl.ClassNames.
Separately Track Performance Metrics and Fit Model
Perform incremental learning on the rest of the data by using the updateMetrics and fit functions. At each iteration:
Simulate a data stream by processing 50 observations at a time.
Call
updateMetricsto update the cumulative and window minimal cost of the model given the incoming chunk of observations. Overwrite the previous incremental model to update the losses in theMetricsproperty. Note that the function does not fit the model to the chunk of data—the chunk is "new" data for the model. Specify the observation weights.Store the minimal cost.
Call
fitto fit the model to the incoming chunk of observations. Overwrite the previous incremental model to update the model parameters. Specify the observation weights.
% Preallocation idxil = ~idxtt; nil = sum(idxil); numObsPerChunk = 50; nchunk = floor(nil/numObsPerChunk); mc = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]); Xil = X(idxil,:); Yil = Y(idxil); Wil = W(idxil); % Incremental fitting for j = 1:nchunk ibegin = min(nil,numObsPerChunk*(j-1) + 1); iend = min(nil,numObsPerChunk*j); idx = ibegin:iend; IncrementalMdl = updateMetrics(IncrementalMdl,Xil(idx,:),Yil(idx), ... 'Weights',Wil(idx)); mc{j,:} = IncrementalMdl.Metrics{"MinimalCost",:}; IncrementalMdl = fit(IncrementalMdl,Xil(idx,:),Yil(idx),'Weights',Wil(idx)); end
IncrementalMdl is an incrementalClassificationNaiveBayes model object trained on all the data in the stream.
Alternatively, you can use updateMetricsAndFit to update performance metrics of the model given a new chunk of data, and then fit the model to the data.
Plot a trace plot of the performance metrics.
h = plot(mc.Variables); xlim([0 nchunk]) ylabel('Minimal Cost') legend(h,mc.Properties.VariableNames) xlabel('Iteration')

The cumulative loss gradually stabilizes, whereas the window loss jumps throughout the training.
Incrementally train a naive Bayes classification model only when its performance degrades.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Configure a naive Bayes classification model for incremental learning so that the maximum number of expected classes is 5, the tracked performance metric includes the misclassification error rate, and the metrics window size is 1000. Fit the configured model to the first 1000 observations.
Mdl = incrementalClassificationNaiveBayes('MaxNumClasses',5,'MetricsWindowSize',1000, ... 'Metrics','classiferror'); initobs = 1000; Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));
Mdl is an incrementalClassificationNaiveBayes model object.
Perform incremental learning, with conditional fitting, by following this procedure for each iteration:
Simulate a data stream by processing a chunk of 100 observations at a time.
Update the model performance on the incoming chunk of data.
Fit the model to the chunk of data only when the misclassification error rate is greater than 0.05.
When tracking performance and fitting, overwrite the previous incremental model.
Store the misclassification error rate and the mean of the first predictor in the second class to see how they evolve during training.
Track when
fittrains the model.
% Preallocation numObsPerChunk = 100; nchunk = floor((n - initobs)/numObsPerChunk); mu21 = zeros(nchunk,1); ce = array2table(nan(nchunk,2),'VariableNames',["Cumulative" "Window"]); trained = false(nchunk,1); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx)); ce{j,:} = Mdl.Metrics{"ClassificationError",:}; if ce{j,2} > 0.05 Mdl = fit(Mdl,X(idx,:),Y(idx)); trained(j) = true; end mu21(j) = Mdl.DistributionParameters{2,1}(1); end
Mdl is an incrementalClassificationNaiveBayes model object trained on all the data in the stream.
To see how the model performance and evolve during training, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(mu21) hold on plot(find(trained),mu21(trained),'r.') xlim([0 nchunk]) ylabel('\mu_{21}') legend('\mu_{21}','Training occurs','Location','best') hold off nexttile plot(ce.Variables) xlim([0 nchunk]) ylabel('Misclassification Error Rate') legend(ce.Properties.VariableNames,'Location','best') xlabel(t,'Iteration')

The trace plot of shows periods of constant values, during which the loss within the previous observation window is at most 0.05.
Input Arguments
Naive Bayes classification model for incremental learning to fit to streaming data,
specified as an incrementalClassificationNaiveBayes model object. You can create
Mdl directly or by converting a supported, traditionally trained
machine learning model using the incrementalLearner function. For more details, see the corresponding
reference page.
Chunk of predictor data to which the model is fit, specified as an
n-by-Mdl.NumPredictors floating-point
matrix.
The length of the observation labels Y and the number of
observations in X must be equal;
Y( is the label of observation
j (row) in j)X.
Note
If Mdl.NumPredictors = 0, fit
infers the number of predictors from X, and sets the corresponding
property of the output model. Otherwise, if the number of predictor variables in the
streaming data changes from Mdl.NumPredictors,
fit issues an error.
Data Types: single | double
Chunk of labels to which the model is fit, specified as a categorical, character, or string array, logical or floating-point vector, or cell array of character vectors.
The length of the observation labels Y and the number of observations in
X must be equal; Y(
is the label of observation j (row) in j)X.
fit issues an error when one or both of these conditions are met:
Ycontains a new label and the maximum number of classes has already been reached (see theMaxNumClassesandClassNamesarguments ofincrementalClassificationNaiveBayes).The
ClassNamesproperty of the input modelMdlis nonempty, and the data types ofYandMdl.ClassNamesare different.
Data Types: char | string | cell | categorical | logical | single | double
Chunk of observation weights, specified as a floating-point vector of positive values.
fit weighs the observations in X
with the corresponding values in Weights. The size of
Weights must equal n, the number of
observations in X.
By default, Weights is ones(.n,1)
For more details, including normalization schemes, see Observation Weights.
Data Types: double | single
Note
If an observation (predictor or label) or weight contains at
least one missing (NaN) value, fit ignores the
observation. Consequently, fit uses fewer than n
observations to create an updated model, where n is the number of
observations in X.
Output Arguments
Updated naive Bayes classification model for incremental learning, returned as an
incremental learning model object of the same data type as the input model
Mdl, an incrementalClassificationNaiveBayes object.
In addition to updating distribution model parameters, fit performs the following actions when Y contains expected, but unprocessed, classes:
If you do not specify all expected classes by using the
ClassNamesname-value argument when you create the input modelMdlusingincrementalClassificationNaiveBayes,fit:Appends any new labels in
Yto the tail ofMdl.ClassNames.Expands
Mdl.Costto a c-by-c matrix, where c is the number of classes inMdl.ClassNames. The resulting misclassification cost matrix is balanced.Expands
Mdl.Priorto a length c vector of an updated empirical class distribution.
If you specify all expected classes when you create the input model
Mdlor convert a traditionally trained naive Bayes model usingincrementalLearner, but you do not specify a misclassification cost matrix (Mdl.Cost),fitsets misclassification costs of processed classes to1and unprocessed classes toNaN. For example, iffitprocesses the first two classes of a possible three classes,Mdl.Costis[0 1 NaN; 1 0 NaN; 1 1 0].
More About
In the bag-of-tokens model, the value of predictor j is the nonnegative number of occurrences of token j in the observation. The number of categories (bins) in the multinomial model is the number of distinct tokens (number of predictors).
Tips
Unlike traditional training, incremental learning might not have a separate test (holdout) set. Therefore, to treat each incoming chunk of data as a test set, pass the incremental model and each incoming chunk to
updateMetricsbefore training the model on the same data.
Algorithms
If predictor variable j has a conditional normal distribution (see the DistributionNames property), the software fits the distribution to the data by computing the class-specific weighted mean and the biased (maximum likelihood) estimate of the weighted standard deviation. For each class k:
The weighted mean of predictor j is
where wi is the weight for observation i. The software normalizes weights within a class such that they sum to the prior probability for that class.
The unbiased estimator of the weighted standard deviation of predictor j is
If all predictor variables compose a conditional multinomial distribution (see the
DistributionNames property), the software fits the distribution
using the Bag-of-Tokens Model. The software stores the probability
that token j appears in class k in the
property
DistributionParameters{.
With additive smoothing [1], the estimated probability isk,j}
where:
which is the weighted number of occurrences of token j in class k.
nk is the number of observations in class k.
is the weight for observation i. The software normalizes weights within a class so that they sum to the prior probability for that class.
which is the total weighted number of occurrences of all tokens in class k.
If predictor variable j has a conditional multivariate
multinomial distribution (see the DistributionNames property), the
software follows this procedure:
The software collects a list of the unique levels, stores the sorted list in
CategoricalLevels, and considers each level a bin. Each combination of predictor and class is a separate, independent multinomial random variable.For each class k, the software counts instances of each categorical level using the list stored in
CategoricalLevels{.j}The software stores the probability that predictor
jin classkhas level L in the propertyDistributionParameters{, for all levels ink,j}CategoricalLevels{. With additive smoothing [1], the estimated probability isj}where:
which is the weighted number of observations for which predictor j equals L in class k.
nk is the number of observations in class k.
if xij = L, and 0 otherwise.
is the weight for observation i. The software normalizes weights within a class so that they sum to the prior probability for that class.
mj is the number of distinct levels in predictor j.
mk is the weighted number of observations in class k.
For each conditional predictor distribution, fit computes the weighted average and standard deviation.
If the prior class probability distribution is known (in other words, the prior distribution is not empirical), fit normalizes observation weights to sum to the prior class probabilities in the respective classes. This action implies that the default observation weights are the respective prior class probabilities.
If the prior class probability distribution is empirical, the software normalizes the specified observation weights to sum to 1 each time you call fit.
References
[1] Manning, Christopher D., Prabhakar Raghavan, and Hinrich Schütze. Introduction to Information Retrieval, NY: Cambridge University Press, 2008.
Version History
Introduced in R2021aStarting in R2021b, naive Bayes incremental fitting functions fit and updateMetricsAndFit compute
biased (maximum likelihood) estimates of the weighted standard deviations for conditionally
normal predictor variables during training. In other words, for each class
k, incremental fitting functions normalize the sum of square weighted
deviations of the conditionally normal predictor
xj by the sum of the weights in class
k. Before R2021b, naive Bayes incremental fitting functions computed
the unbiased standard deviation, like fitcnb. The currently returned weighted standard deviation estimates differ
from those computed before R2021b by a factor of
The factor approaches 1 as the sample size increases.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)