In Chess, performance isn't measured absolutely; it is inferred from wins (1), losses (0), and draws (0.5) against other players. A player's rating depends on the ratings of their opponents, and the results scored against them. The difference in rating between two players determines an estimate for the expected score between them.
Supposing Player A was expected to score Ea points (but actually scored Sa).
The formula for updating his rating is :
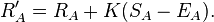
This update can be performed after each game or each tournament, or after any suitable rating period.
Suppose Player A has a rating Ra of 1613, and plays in a five-round tournament. He (or she) loses to a player rated 1609, draws with a player rated 1477, defeats a player rated 1388, defeats a player rated 1586, and loses to a player rated 1720. The player's actual score Sa is (0 + 0.5 + 1 + 1 + 0) = 2.5. The expected score Ea , calculated according to the formula see in Problem 3056, was (0.506 + 0.686 + 0.785 + 0.539 + 0.351) = 2.867. Therefore the player's new rating R'a is (1613 + 32×(2.5 − 2.867)) = 1601. We assume that the K factor is always 32.
I give you rating of Player A, ratings of their opponents and results.
Compute the new rating (K = 32).
Solution Stats
Problem Comments
Solution Comments
Show commentsProblem Recent Solvers65
Suggested Problems
-
3082 Solvers
-
1359 Solvers
-
2272 Solvers
-
Magic is simple (for beginners)
11164 Solvers
-
1029 Solvers
More from this Author43
Problem Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!
In the second test, there are four players and five game results.
A delightful series of problems. I especially like the tests with real-world examples.
Fixed. Thank you Andrew.
Hum, real life doesn't round up scores. And usually our rating is updated after each match (as it is in cody).