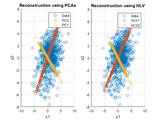
Principal Component Analysis / Hebbian-based Max Eigenfilter
% TASK 1. Let’s generate 800 random data on a 2-dimensional plane. The data
% are generated as 4 clusters, of which centers are located at (2,2), (-1,-2),
% (2,0) and (0,1). Each cluster has 200 data, of which distances from each
% center are randomly distributed with Gaussian distribution (standard
% deviation = 2, 2, 1, and 1, respectively).
% TASK 1-(a) Mark the generated data with dots (or circles) on a
% 2-dimensional space.
% TASK 1-(b) Conduct Principal Component Analysis based on eigenvector
% analysis. (You may use any library function for the
% eigenvector/eigenvalue calculation.) Show the principal axes and data
% projects on the axes.
% TASK 1-(c) Program and calculate the Hebbian-based maximum eigenfilter,
% and compare with the principal in (b).
Cite As
Shujaat Khan (2025). Principal Component Analysis / Hebbian-based Max Eigenfilter (https://au.mathworks.com/matlabcentral/fileexchange/72052-principal-component-analysis-hebbian-based-max-eigenfilter), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- AI and Statistics > Statistics and Machine Learning Toolbox > Dimensionality Reduction and Feature Extraction >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Principal Component Analysis and Hebbian-based Maximum Eigenfilter
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0 |