1-D Multisignal Analysis

This section takes you through the features of 1-D multisignal wavelet analysis, compression and denoising using the Wavelet Toolbox™ software. The rationale for each topic is the same as in the 1-D single signal case.

The toolbox provides the following functions for multisignal analysis.

Analysis-Decomposition and Synthesis-Reconstruction Functions

Function Name	Purpose
mdwtdec	Multisignal wavelet decomposition
mdwtrec	Multisignal wavelet reconstruction and extraction of approximation and detail coefficients

Decomposition Structure Utilities

Function Name	Purpose
chgwdeccfs	Change multisignal 1-D decomposition coefficients
wdecenergy	Multisignal 1-D decomposition energy repartition

Compression and Denoising Functions

Function Name	Purpose
mswcmp	Multisignal 1-D compression using wavelets
mswcmpscr	Multisignal 1-D wavelet compression scores
mswcmptp	Multisignal 1-D compression thresholds and performance
wdenoise	Wavelet signal denoising
mswthresh	Perform multisignal 1-D thresholding

1-D Multisignal Analysis

Load an image file, and display its dimensions. For purposes of this example, unless stated otherwise, you will treat the data as a multisignal. Each row of the image is one signal.

load thinker
size(X)

ans = 1×2

   192    96

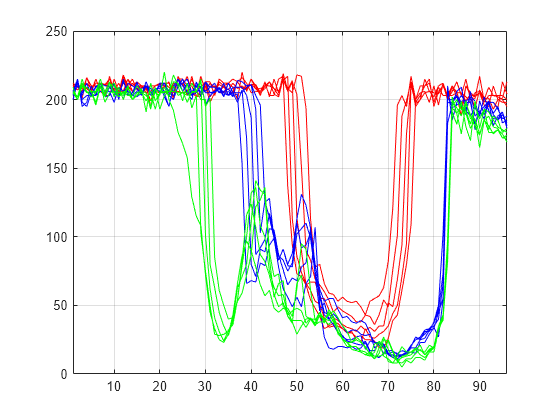
Plot some signals from the data.

plot(X(1:5,:)',"r")
hold on 
plot(X(21:25,:)',"b")
plot(X(31:35,:)',"g")
hold off
xlim([1 96])
grid on

Decomposition and Reconstruction

Use mdwtdec to perform a wavelet decomposition of the multisignal at level 2 using the db2 wavelet.

dec = mdwtdec("r",X,2,"db2")

dec = struct with fields:
        dirDec: 'r'
         level: 2
         wname: 'db2'
    dwtFilters: [1x1 struct]
       dwtEXTM: 'sym'
      dwtShift: 0
      dataSize: [192 96]
            ca: [192x26 double]
            cd: {[192x49 double]  [192x26 double]}

Use chgwdeccfs to generate a new wavelet decomposition structure from dec. For each signal, change the wavelet coefficients by setting all the coefficients of the detail of level 1 to zero.

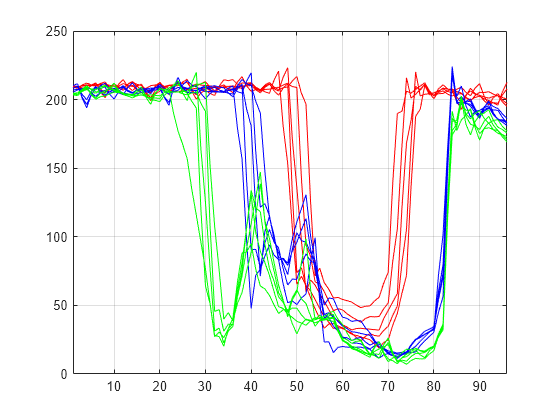
decBIS = chgwdeccfs(dec,"cd",0,1);

Use mdwtrec to perform a wavelet reconstruction of the multisignal. Plot some of the new signals.

Xbis = mdwtrec(decBIS); 
plot(Xbis(1:5,:)',"r")
hold on 
plot(Xbis(21:25,:)',"b")
plot(Xbis(31:35,:)',"g")
hold off
grid on
xlim([1 96])

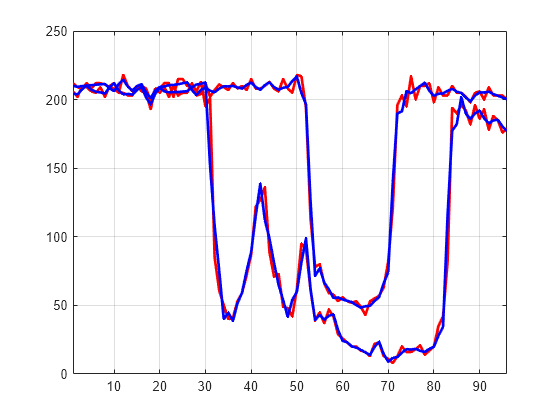
Compare old and new signals by plotting them together.

idxSIG = [1 31]; 
plot(X(idxSIG,:)',"r",LineWidth=2)
hold on 
plot(Xbis(idxSIG,:)',"b",Linewidth=2)
hold off
grid on 
xlim([1 96])

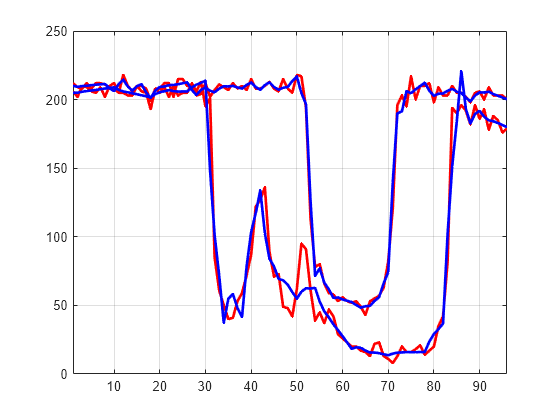
Set the wavelet coefficients at level 1 and 2 for signals 31 to 35 to the value zero, perform a wavelet reconstruction of signal 31, and compare some of the old and new signals.

decTER = chgwdeccfs(dec,'cd',0,1:2,31:35); 
Y = mdwtrec(decTER,'a',0,31);
figure
plot(X([1 31],:)',"r",LineWidth=2)
hold on 
plot([Xbis(1,:); Y]',"b",LineWidth=2) 
hold off
grid on
xlim([1 96])

Use wdecenergy to compute the energy of signals and the percentage of energy for wavelet components. Display the energy of two of the signals.

[E,PEC,PECFS] = wdecenergy(dec);
Ener_1_31 = E([1 31])

Ener_1_31 = 2×1
106 ×

    3.7534
    2.2411

Compute the percentage of energy for wavelet components of signals 1 and 31. The first column shows the percentage of energy for approximations at level 2. Columns 2 and 3 show the percentage of energy for details at level 2 and 1, respectively.

PEC_1_31 = PEC([1 31],:)  

PEC_1_31 = 2×3

   99.7760    0.1718    0.0522
   99.3850    0.2926    0.3225

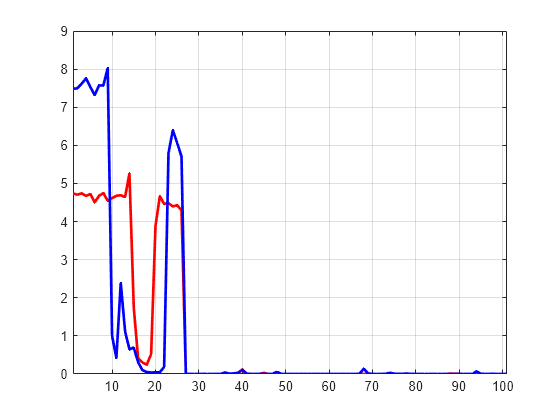
Display the percentage of energy for wavelet coefficients of signals 1 and 31. As we can see in the dec structure, there are 26 coefficients for the approximation and the detail at level 2, and 49 coefficients for the detail at level 1.

PECFS_1 = PECFS(1,:);
PECFS_31 = PECFS(31,:); 
plot(PECFS_1,"r",LineWidth=2)
hold on 
plot(PECFS_31,"b",LineWidth=2)
hold off
grid on
xlim([1 size(PECFS,2)])

Compression

Use mswcmp to compress the signals to obtain a percentage of zeros near 95% for the wavelet coefficients.

[XC,decCMP,~] = mswcmp("cmp",dec,"N0_perf",95); 
[Ecmp,PECcmp,PECFScmp] = wdecenergy(decCMP);

Plot the original signals 1 and 31, and the corresponding compressed signals.

plot(X([1 31],:)',"r",LineWidth=2)
hold on 
plot(XC([1 31],:)',"b",LineWidth=2)
hold off
grid on
xlim([1 96])

Use mswcmptp to compute thresholds, percentage of energy preserved and percentage of zeros associated with the L2_perf method preserving at least 95% of energy.

[THR_VAL,L2_Perf,N0_Perf] = mswcmptp(dec,"L2_perf",95); 
idxSIG = [1,31];
Thr   = THR_VAL(idxSIG)

Thr = 2×1

  256.1914
  158.6085

L2per = L2_Perf(idxSIG) 

L2per = 2×1

   96.5488
   94.7197

N0per = N0_Perf(idxSIG) 

N0per = 2×1

   79.2079
   86.1386

Compress the signals to obtain a percentage of zeros near 60% for the wavelet coefficients.

[XC,decCMP,~] = mswcmp("cmp",dec,"N0_perf",60);

XC signals are the compressed versions of the original signals in the row direction. Compress the XC signals in the column direction

XX = mswcmp("cmpsig","c",XC,"db2",2,"N0_perf",60);

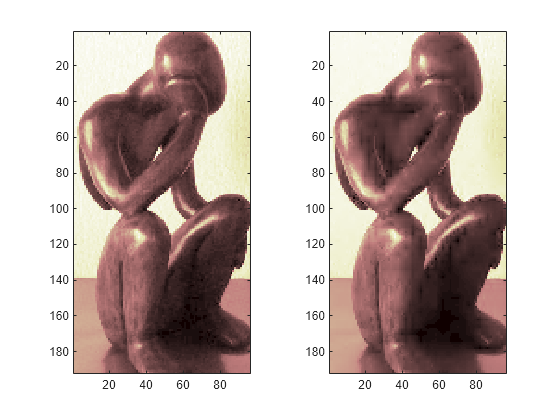
Plot original signals X and the compressed signals XX as images.

tiledlayout(1,2)
nexttile
image(X) 
nexttile
image(XX) 
colormap(pink(222))

Denoising

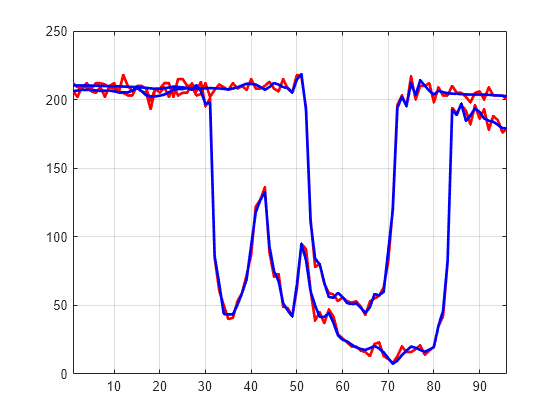
You can use the wdenoise function to denoise a multisignal. By default, wdenoise denoises the columns of matrix. Denoise the multisignal using wdenoise with default settings. Compare with the original signals.

XD = wdenoise(X');
XD = XD';
figure
plot(X([1 31],:)',"r",LineWidth=2)
hold on 
plot(XD([1 31],:)',"b",Linewidth=2)
hold off
grid on
xlim([1 96])

References

[1] Denoeud, L., Garreta, H., and A. Guénoche. "Comparison of Distance Indices Between Partitions." In International Symposium on Applied Stochastic Models and Data Analysis, 432–440. Brest, France: École Nationale des Télécommunications de Bretagne, 2005.